Hydrodynamic stability- Rayleigh equation - Couette flow

In summary, the conversation is about formulating the stability problem in the incompressible inviscid limit and finding the dispersion relation in the Couette flow regime. The speaker mentions using the Rayleigh equation and asks for any references or ideas. The other person suggests searching for "couette flow stability" and mentions the book "Chandrasekhar." The first speaker asks for more specifics and the other person provides a link to the book.
  • #1
URIA
6
0
TL;DR Summary
Folks,
I'm trying to formulate the stability problem in the incompressible inviscid limit and find the dispersion relation in the Couette flow regime. As shown, the 2 infinite plates move one against the other, unlike the "standard" case where one plate is static and the second moves. I'm trying to use the Rayleigh equation but I'm not sure how to do this.

Any references or ideas are welcome :)
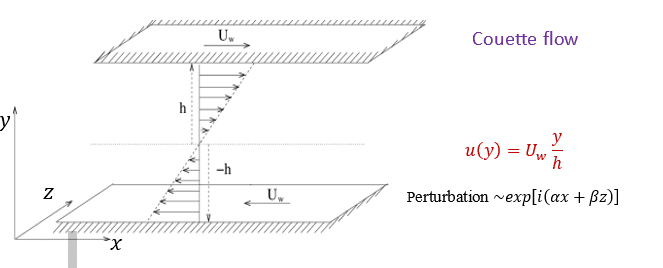
Folks,
I'm trying to formulate the stability problem in the incompressible inviscid limit and find the dispersion relation in the Couette flow regime. As shown, the 2 infinite plates move one against the other, unlike the "standard" case where one plate is static and the second moves. I'm trying to use the Rayleigh equation but I'm not sure how to do this.
Any references or ideas are welcome :)

1673202054928.png
 
Physics news on Phys.org
  • #2
If you google ”couette flow stability” plenty of references come up.
 
  • #3
Should I assume you've already explored references like Chandrasekhar?
 
  • #4
boneh3ad said:
Should I assume you've already explored references like Chandrasekhar?
No, can you be more specific?
 
  • #6
Much Appreciated!
 

FAQ: Hydrodynamic stability- Rayleigh equation - Couette flow

What is hydrodynamic stability?

Hydrodynamic stability refers to the study of the behavior of fluid flows and their tendency to either remain steady or become turbulent. It involves analyzing whether small disturbances in a flow will grow over time, leading to a transition from laminar (smooth) to turbulent (chaotic) flow, or whether they will decay, allowing the flow to remain stable and laminar.

What is the Rayleigh equation in the context of hydrodynamic stability?

The Rayleigh equation is a differential equation used in the study of the stability of inviscid (non-viscous) fluid flows. It describes the behavior of small disturbances in a flow and is derived from the linearization of the Navier-Stokes equations under the assumption of inviscid flow. The Rayleigh equation helps determine whether a given flow profile is stable or unstable to infinitesimal disturbances.

What is Couette flow?

Couette flow refers to the flow of a viscous fluid between two parallel surfaces, where one surface is stationary, and the other is moving at a constant velocity. This type of flow is often used as a model for studying shear-driven flows and is characterized by a linear velocity profile in the case of simple Couette flow. It serves as a fundamental example in fluid dynamics and hydrodynamic stability studies.

How is the stability of Couette flow analyzed using the Rayleigh equation?

The stability of Couette flow can be analyzed using the Rayleigh equation by examining the base flow profile, which in the case of simple Couette flow is linear. By substituting this velocity profile into the Rayleigh equation, one can study the behavior of small perturbations. For inviscid Couette flow, the Rayleigh equation reveals that the flow is neutrally stable, meaning that small perturbations neither grow nor decay, indicating marginal stability.

What are the practical implications of hydrodynamic stability analysis in engineering?

Hydrodynamic stability analysis has significant practical implications in engineering, particularly in the design and optimization of fluid systems. Understanding the stability of fluid flows helps engineers predict and control transition to turbulence, which can affect the efficiency and performance of various systems, such as pipelines, aircraft, and marine vessels. It also aids in the development of strategies to mitigate undesirable flow behaviors, ensuring safe and efficient operation of fluid-related technologies.

Similar threads

I Can Couette Flow with Wavy Plates?
Replies
12
Views
1K
How to Determine the Stability Condition in Couette Flow?
Replies
2
Views
1K
I Work - Energy Principle Application to Fluid Flow
2
Replies
48
Views
3K
What Equations Govern This Hypothetical Fluid Flow?
Replies
1
Views
794
A Sufficient conditions for Rayleigh-Taylor instability
Replies
1
Views
1K
A How to Solve Isothermal Incompressible Navier-Stokes for Compressible Fluid?
Replies
20
Views
5K
Computational Fluid Dynamics - Couette flow & Reynolds Number
Replies
1
Views
4K
Does Fluid Dynamics Explain Pressure Gradients in a Frictionless Tube?
2
Replies
48
Views
4K
Numerical solution to stationary viscous flow with a Darcy term
Replies
14
Views
16K
Bernoulli to explain Magnus Effect
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top