Hydrodynamics - Wave of Translation

Click For Summary

Discussion Overview

The discussion revolves around the hydrodynamics of a ship moving in shallow water, specifically focusing on the behavior of wave patterns created by the ship, including the disappearance of transverse waves when the ship exceeds a certain speed. Participants explore the implications of critical speed in wave dynamics and draw parallels to other contexts, such as supersonic flight.

Discussion Character

  • Exploratory, Technical explanation, Debate/contested

Main Points Raised

  • One participant notes that in deep water, a ship creates two wave patterns: transverse and divergent, at an angle of 19°28'.
  • Another participant suggests that the transverse wave does not disappear but transforms into a shock wave or bore when the ship exceeds the critical speed of ##\sqrt{gh}##.
  • A different participant references a video that states supercritical speed results in divergent waves at approximately a 45-degree angle, but clarifies that this angle occurs only when the ship's speed is 1.4 times the critical speed.
  • One participant posits that the absence of transverse waves is due to the ship exceeding the velocity of these waves, implying that no new transverse wake is generated after the ship passes.
  • Another participant discusses the physics of tidal bores and suggests that the leading transverse wave is not significant in open water, contrasting it with the behavior of waves in confined channels or at shorelines.

Areas of Agreement / Disagreement

Participants express differing views on whether transverse waves disappear or transform into shock waves, indicating that multiple competing perspectives remain unresolved in the discussion.

Contextual Notes

Participants reference critical speed and wave behavior without fully resolving the implications of these concepts, and there are mentions of specific conditions under which certain wave behaviors occur, such as in confined channels or at shorelines.

jaumzaum
Messages
433
Reaction score
33
Hello guys!

ake-pattern-of-transverse-and-divergent-waves_Q640.jpg

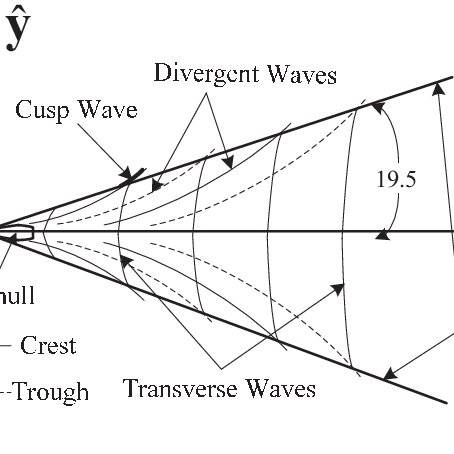
I am studying the hydrodynamics of a ship in shallow water. In deep water the ship creates 2 wave patterns, one transverse and another divergent, both making an angle of 19°28'. Also, the maximum velocity of a wave in shallow water is given by ##\sqrt{gh}## where h is the depth of the water.

The part that I don't understand is why transverse the wave disappears if the ship starts moving faster than ##\sqrt{gh}## ?

I think that could happen in a plane also (but I am not sure), in the case the plane becomes supersonic.
 
Last edited:
Physics news on Phys.org
I'm not sure you could say the transverse wave disappears. A kind of 'shock wave' or bore (if you can call it that) in front of the ship (a soliton apparently). This is because sqrt(gh) is the critical speed at which waves travel through the water at that depth. See this video:
 
Thanks @Arjan82, excellent video.

Note at 3:06 the video says "supercritical speed: divergent waves are issued at approximately a 45 degree angle, having absorbed the transverse waves"

Actually the 45 degree angle only occurs when ## v_{ship}/\sqrt{gh} = 1,4 ##

1637721229872.png


Also, one of the most important books in the topic ( Principles of Naval Arquitecture) says

1637721186573.png

1637721209837.png
That's why I think they actually disappears. But they don't provide a decent explanation. Ould you think of one?
 
Well, I think that what they are not showing here is the transversal wave that is in front of the ship (also see the video). This is a kind of shock wave because the ship is exceeding the transversal wave velocity. So by the time the ship has past the damage, so to speak, is already done and no other transversal wake is generated.
 
I believe the physics of the tidal bore (which is often a "step"wave) require a confined channel as shown on the video. Also breaking waves on a shore are truly shock waves because of the slope (decreasing h) of the shoreline. In my experience the leading transverse wave is not very noticeable on open water shallow or not.
 

Similar threads

Undergrad Shallow Water Wave Equation Simulation: Reverse Shoaling?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad When is a water surface not dispersive?
  • · Replies 1 ·
Replies
1
Views
1K
Graduate Refraction of Ocean waves: Wide Headland vs Narrow
  • · Replies 22 ·
Replies
22
Views
8K
Graduate Tsunami Waves & Mechanical Wave Physics
  • · Replies 21 ·
Replies
21
Views
14K
Undergrad Some questions regarding Acoustic wave reflection
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad How do submarines communicate with radio waves?
  • · Replies 36 ·
2
Replies
36
Views
6K
Graduate Longitudinal waves and vector potentials.
  • · Replies 3 ·
Replies
3
Views
2K
Waves high school question -- Book answers are totally rubbish
  • · Replies 61 ·
3
Replies
61
Views
6K
Undergrad Discussion on the probabilistic interpretation of quantum mechanics
  • · Replies 11 ·
Replies
11
Views
1K
Graduate Diffraction theory, power density and angle of incidence
  • · Replies 5 ·
Replies
5
Views
3K