Hydrostatic forces on a curved surface

[rcummings89]

Hello,

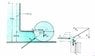
I'm trying to go through an example problem in a fluid dynamics textbook, and I'm having trouble understanding some of their logic. The problem deals with a solid cylinder of radius 0.8 m hinged at its midpoint that opens when the water it holds back reaches 5 m, and it is asking for the hydro-static forces acting on the cylinder, where the center of the cylinder is 4.2 m below the surface (see attached picture).

Their solution...

For the horizontal force: F_x = F_H = ρgh_cA = (1000 kg/m³) (9.81 m/s²) [4.2 m + (0.8 m/2)] (0.8 m*1 m)

Now, I understand it up until the last part that deals with the area. Firstly, the 1 m length is never mentioned, is this just a typical assumption? Also (probably me missing something very basic here) but what area is radius * length?

For F_y they use the same area component, but when they calculate the weight they use the formula:

W = ρgV = ρg(R² - πR²/4)(1) = (1000 kg/m³) (9.81 m/s²) (0.8 m)² (1-π/4) (1 m)

And again, my question is, what area are they using (multiplied by 1 m) to calculate the volume?

Thanks in advance!

 

[SteamKing]

1. If you are not told the length of the apparatus, then a per meter basis (or L = 1 m) is reasonable, assuming no changes in the shape of the apparatus.
2. The Area = R * L is the projected area at the bottom of the outlet (see the inset figure in the lower right hand corner of your attachment.
3. Again, see the lower right hand corner of your attachment. The weight they are calculating is that of the lightly shaded portion where the letter 'W' is located.

 

[rcummings89]

Ok, I think I understand. When they say "R" I kept thinking of circles and kept trying to find area formulas related to circles. I didn't realize they were just using R as the length of the side...

Thanks SteamKing!