Hyperbola's asymptote, where's my mistake?

[Poznerrr]

I have tried like 5 times to do this problem ans still don't get the answer I'm supposed to (A). Anybody finds mistake in my work below?

 

[Fightfish]

If I'm not mistaken, it should be $a/b$ and not $b/a$. so the factor appearing will be $2/3$ and not $3/2$.

 

[Poznerrr]

If I'm not mistaken, it should be $a/b$ and not $b/a$. so the factor appearing will be $2/3$ and not $3/2$.

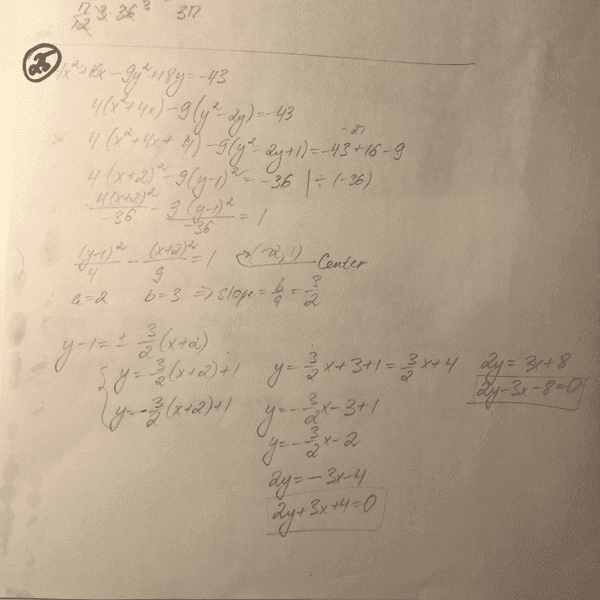
Yeah, I thought about it, and it works out with a/b being the slope of the asymptote. But different sources stick to either a/b and b/a, so it's really confusing which slope is actually correct.

 

[Fightfish]

Yeah, I thought about it, and it works out with a/b being the slope of the asymptote. But different sources stick to either a/b and b/a, so it's really confusing which slope is actually correct.

The way to remember it is well, to derive it yourself, which isn't very hard. The general equation for a hyperbola is in the form
\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1
In the asymptotic limit, the term $1$ becomes insignificant and so we drop it, leaving
\frac{y^2}{a^2} = \frac{x^2}{b^2}
and so
y = \pm \frac{a}{b} x

 

[micromass]

Given a conic section
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
the asymptotes can be calculated by a little trick. Basically, the slope of the asymptote is $s$, where $s$ is the solution to $A + Bs + Cs^2=0$.

In your case, this corresponds to the solution of $4-9s^2=0$. So we get $s = 2/3$ or $s= -2/3$. The slope of (A) is $-2/3$.

 

[member 587159]

Given a conic section
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
the asymptotes can be calculated by a little trick. Basically, the slope of the asymptote is $s$, where $s$ is the solution to $A + Bs + Cs^2=0$.

In your case, this corresponds to the solution of $4-9s^2=0$. So we get $s = 2/3$ or $s= -2/3$. The slope of (A) is $-2/3$.

Ah, the trick with the homogeneous coordinates and equations ;)

 

[Poznerrr]

Given a conic section
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
the asymptotes can be calculated by a little trick. Basically, the slope of the asymptote is $s$, where $s$ is the solution to $A + Bs + Cs^2=0$.

In your case, this corresponds to the solution of $4-9s^2=0$. So we get $s = 2/3$ or $s= -2/3$. The slope of (A) is $-2/3$.

Thanks! I'll use this trick in future.

 

[micromass]

Thanks! I'll use this trick in future.

You shouldn't unless you can prove the trick actually works.

 

[Irene Kaminkowa]

Poznerrr,
For the proof, divide the initial conic section by x². And find the limit if x->infinity. Thus, your get the equation from post #5, where s = y/x, that is the slope.

 

[Ray Vickson]

Thanks! I'll use this trick in future.

Also: in the future do not post images of your work, as most people on this Forum will not read them and will not be willing to help you. Just type out your work.