- #1
LogicX
- 181
- 1
http://i254.photobucket.com/albums/hh116/balthamossa2b/1290457745312.jpg
Can someone explain the flaw in this logic?
Can someone explain the flaw in this logic?
Grep said:I think of it this way. Since "removing" the corners like that doesn't change the perimeter at all, it will fail to converge on the perimeter of a circle. So it's rather unlike, say, increasing the number of sides of a polygon inside the circle. That one converges on the real perimeter. His example does not.
D H said:What do you mean by "real", Jarle? What makes the Euclidean norm more real than the taxicab norm?
What is the circumference of the curve x2+y2=r2 using the taxicab norm?
Grep said:Another thing my friend pointed out is that, the perimeter he's calculating is always 4. Then he concludes that pi = 4. But pi is HALF the circumference. The perimeter of the circle would be 4, which means if 2*pi = perimeter then pi = (perimeter / 2) = (4 / 2) = 2. Silly of me not to notice that obvious problem.
But it sounds better to say pi = 4 for the purposes of confusing people, I suppose.
I kind of see your point. But it's, IMO, nitpicking of the highest order. Let's assume I have a perfect unit circle drawn out (or to well within the tolerances with which I will measure). I can also measure the circumference to a certain precision. Which means I can empirically determine PI to whatever the limits of my measurement and my ability to get a perfect unit circle. Won't get me there exactly, but neither will any other method since it's an irrational number. All I can do is compute it to a certain number of decimal points.Jarle said:I mean what he calls "real" is more correctly put as "conventional", since there is no pre-existing platonic length of the circle independent of our ways of "finding" it. The choice of the euclidean norm is conventional as a measure of length (which is commonly understood by length unless otherwise is stated), it is not measuring real lengths as opposed to other norms. Similarly, approximating with regular polygons doesn't measure real length as opposed to other limiting sums. They measure different things, but none of them are more real than the other.
And? That means the sides of the initial square are of length 1. Which means it's perimeter is 4 throughout. And since the perimeter will always be 4, we would have to derive a pi which is half that, following his logic (which is obviously totally wrong).Jarle said:The diameter in the drawing is set as 1. Besides, the resulting ratio must be larger than pi since the measured length is constantly larger.
Grep said:I kind of see your point. But it's, IMO, nitpicking of the highest order. Let's assume I have a perfect unit circle drawn out (or to well within the tolerances with which I will measure). I can also measure the circumference to a certain precision. Which means I can empirically determine PI to whatever the limits of my measurement and my ability to get a perfect unit circle. Won't get me there exactly, but neither will any other method since it's an irrational number. All I can do is compute it to a certain number of decimal points.
It's real in the sense that if I compute it and it disagrees with my empirical measurement within my level of accuracy, I would have to conclude that my computation is wrong. Either that, or define a circle as something which has no relation to the real world, which wouldn't be very useful. And I mean "real" in that sense, and that sense only.
Grep said:And? That means the sides of the initial square are of length 1. Which means it's perimeter is 4 throughout. And since the perimeter will always be 4, we would have to derive a pi which is half that, following his logic (which is obviously totally wrong).
Apologies, on that one I have to agree with you 100%. I clearly mixed up r and d. My fault for assuming my friend got it right and not thinking it through for myself (not a regular habit I assure you...Jarle said:No, since pi is defined as the perimeter divided by the diameter. In this case the perimeter equals pi, since the diameter is 1. pi is only only half the perimeter if the diameter is 2 (2*r*pi =d*pi = 1*pi = pi).
 ).
).Curl said:It's an infinitely zigzag path, of course the length is longer. You can make a zigzag path of infinite length but still be finite in "size" if you will.
DaveC426913 said:This is a simpler problem wrapped in a complex cloak.
Start with a square 1 unit on a side.
You can perform the same staircasing, and it would appear that the diagonal has a length of 2.
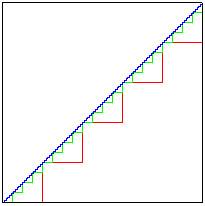
The key is that 'a zig zag line with an arbitrarily large number of vanishingly small zigs and zags' is not the same as 'a diagonal line'.
It does have a length of 2 -- using the taxicab, or L1, norm, that is. What this troll physics shows is that the circumference of a circle using the taxicab norm is c=4d. That does not mean that pi is 4. It just means that different norms will yield different answers for length.DaveC426913 said:This is a simpler problem wrapped in a complex cloak.
Start with a square 1 unit on a side.
You can perform the same staircasing, and it would appear that the diagonal has a length of 2.
lugita15 said:I don't really see any kind of paradox here. Just because you have a parametric curve [tex]f : [0,1] \rightarrow \Re^{2}[/tex] whose graph is a circle of radius r doesn't mean the arc length of f is [tex]2 \pi r[/tex]. For instance, f could go around the unit circle multiple times. So it may be true that the sequence of jagged figures "converges" in some sense to a parametrization of a circle, but it can have a different arc length.
Dadface said:Jarle,the length of the jagged path does not converge,the length is equal to 4 and remains at 4 no matter how many zig zags are used.
D H said:It does have a length of 2 -- using the taxicab, or L1, norm, that is. What this troll physics shows is that the circumference of a circle using the taxicab norm is c=4d. That does not mean that pi is 4. It just means that different norms will yield different answers for length.
DaveC426913 said:Well, the "diagonal" of a square is a straight line between two opposing corners, so it will not have a length of 2.
But they don't converge on the euclidean norm.Jarle said:Note that the limit of these jagged paths is the true diagonal; they converge uniformly to the line in the euclidean norm.
That diagonal line does have a length of 2 using the L1 norm.DaveC426913 said:Well, the "diagonal" of a square is a straight line between two opposing corners, so it will not have a length of 2.D H said:It does have a length of 2 -- using the taxicab, or L1, norm, that is. What this troll physics shows is that the circumference of a circle using the taxicab norm is c=4d. That does not mean that pi is 4. It just means that different norms will yield different answers for length.
DaveC426913 said:But they don't converge on the euclidean norm.
No matter how small you make the increment, the "taxi-cab diagonal" is always exactly 2.