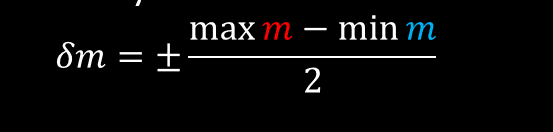I'm confused on which equation gives percentage uncertainty

  • Context: Undergrad 
  • Thread starter Thread starter homeworkhelpls
  • Start date Start date
  • Tags Tags
    Confused Uncertainty
Click For Summary

Discussion Overview

The discussion revolves around the calculation of percentage uncertainty in the context of determining the slope (gradient) from a graph. Participants explore different equations and methods for estimating uncertainty related to best-fit lines and data points.

Discussion Character

  • Exploratory
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • Some participants express confusion about which equation to use for calculating percentage uncertainty.
  • One participant suggests that the equations may refer to different methods for determining the slope, with implications for how uncertainty is calculated.
  • Another participant questions the context of the equations and the assumptions behind determining the best line through data points.
  • There is a suggestion that the method used to find the best line affects which equation should be applied.
  • One participant raises concerns that a simplified procedure might overestimate the uncertainty.
  • A later reply asks for clarification on what the max and min slopes represent, indicating a need for more information to provide a proper answer.
  • Another participant hints at considering the units involved in percentage versus absolute uncertainty.

Areas of Agreement / Disagreement

Participants do not reach a consensus on which equation is appropriate for calculating percentage uncertainty, and multiple competing views regarding the methods and assumptions remain unresolved.

Contextual Notes

Limitations include a lack of clarity on the definitions of the slopes being discussed and the specific context in which the equations are applied. There are unresolved questions about the statistical distribution of the slopes.

homeworkhelpls
Messages
41
Reaction score
1
im confused about the difference of this equation:
1665243195922.png

and this one:
1665243195935.png

which gives percentage uncertainty, so which one should be used to calculate the uncertainty?
 
Last edited:
Physics news on Phys.org
Are you trying to compute the average gradient?

or are you trying to find the best line through a set of data points plotted in XY form?
 
my bad I am trying to find the uncertainty from the graph
 
The two equations are out of context but my guess is that they refer to different methods of determining the slope (gradient). It looks like the second equation assumes that one knows the best line (determined how?) while the first equation assumes that one draws two eyeballed straight lines that pass reasonably well over the data such that the best line has a slope between them. Which one you use depends on your method of finding the best line.
 
Reply
  • Like
Likes   Reactions: TSny and robphy
kuruman said:
The two equations are out of context but my guess is that they refer to different methods of determining the slope (gradient). It looks like the second equation assumes that one knows the best line (determined how?) while the first equation assumes that one draws two eyeballed straight lines that pass reasonably well over the data such that the best line has a slope between them. Which one you use depends on your method of finding the best line.
no sorry bro i don't think you understand it very well i mean the uncertainty and best fit is just determined by drawing the line, thanks for the help though
 
Reply
  • Sad
Likes   Reactions: robphy
It almost certainly looks like a simplified procedure that likely overestimates the uncertainty.
 
homeworkhelpls said:
which one should be used to calculate the uncertainty?
I assume that you mean the standard uncertainty of the slope.

You have not provided enough information. What do these max and min slopes represent? Are they slopes from a 95% confidence interval around the fitted slope parameter. Are they slopes takin men directly from the data? Do you have any other estimate that could describe the statistical distribution from which these slopes are drawn?
 
Hint: Think about the units.

What units would you expect a percentage uncertainty to have versus an absolute uncertainty?
 

Similar threads

Undergrad Reported uncertainties for time and distance in physics experiment
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Uncertainty in measurements of the thickness of a pile of pellets
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad Measurement for uncertainty in nonlinear model
  • · Replies 4 ·
Replies
4
Views
2K
I'm getting two possible uncertainties for frequency
  • · Replies 8 ·
Replies
8
Views
2K
Understanding the Proper Uncertainty Formula to Use
  • · Replies 4 ·
Replies
4
Views
1K
Is my textbook wrong about absolute uncertainties?
  • · Replies 2 ·
Replies
2
Views
1K
How to teach errors and uncertainty in an undergraduate setting?
  • · Replies 2 ·
Replies
2
Views
897
Undergrad Heisenberg uncertainty principle and the canonical momentum operator
  • · Replies 32 ·
2
Replies
32
Views
3K
Undergrad Monte Carlo for uncertainty estimation
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Piecewise linear interpolation with uncertainties
  • · Replies 5 ·
Replies
5
Views
2K