Implementing the PSD from its definition

[james1234]

I would be grateful for some direction on this.

I wish to implement the following -
Given a deterministic signal (the feedback signal of a closed-loop stable system) I would like to plot the power spectral density.
The definition I am working with is this:

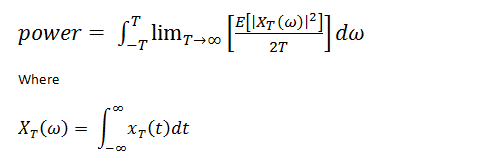
Implementation (MATLAB):

% Given a signal the plot of the power spectral density over the frequency range 0.1-5 rad/s is given by
% The continuous time Fourier transform

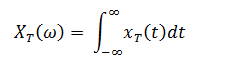
w=.1:.1:5; % 0.1 to 5 rad/s (frequency range of interest)

% Compute the transform
for ii=1:50 % For each frequency increment (50 samples over the interval 0.1:0.1:5)

yy1=um.*sin(w(ii)*t) % where t is a vector of dimension [1, 3610] and um is the time series in question
yy2=um.*cos(w(ii)*t) %

% the intergral
yi1=trapz(t,yy1);
yi2=trapz(t,yy2);

% square of the Fourier transform i.e. |X(omega)|^2
trans(ii)=(yi1^2+yi2^2);

end

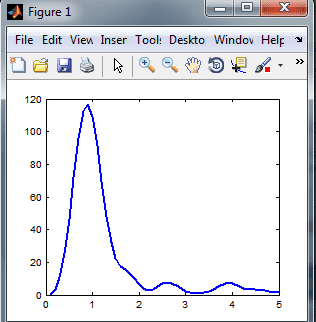
figure(1)
plot(w, trans) % |X(omega)|^2

% For a deterministic signal no need to compute the expected value, the power of the signal is instead given by

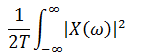
% Energy: integral of the square of the Fourier transform wrt to frequency
energy = trapz(w, trans);
figure(2)
plot(w,energy) % sadly things have gone awry HERE!

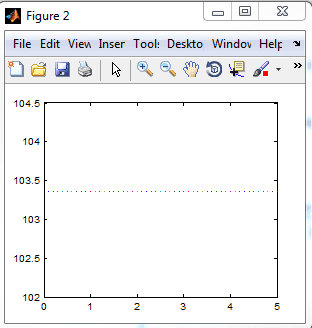% Power
power = energy / t(end); % where t(end) is the duration of the signal in question
figure(3)
plot(w, power)
The PSD should be a real valued nonnegative function of omega not a constant. Any prompts would be much appreciated!

 

[jasonRF]

The energy of a signal is a single number - a scalar. It is not a function of frequency. After all you integrated over frequency already in order to compute it! Look at numel(energy) and you should see that it is has 1 element.