student34
- 639
- 21
This is just a rough estimate of what a simple bock universe might be to an observer in the red worldline on the left side, and what it is to an observer in one of the blue worldlines in the graph on the right side. In the graph on the left side, two blue objects moved past the red object very quickly. And the graph on the right, the red object moves past the blue objects very quickly.
(Please just assume there is sufficient depth for the redline to go behind the blue lines, but insignificant enough to change anything about the graphs)
In what formation does this block universe exist?
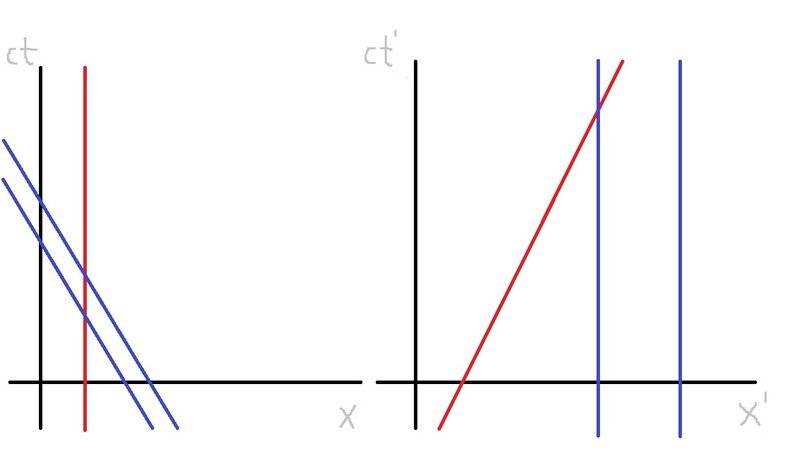
(Please just assume there is sufficient depth for the redline to go behind the blue lines, but insignificant enough to change anything about the graphs)
In what formation does this block universe exist?