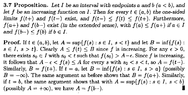Increasing Function on an Interval .... Browder, Proposition 3.7 .... ....

[Math Amateur]

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 3: Continuous Functions on Intervals and am currently focused on Section 3.1 Limits and Continuity ... ...

I need some help in understanding the proof of Proposition 3.7 ...Proposition 3.7 and its proof read as follows:View attachment 9509
In the above proof by Andrew Browder we read the following:

" ... ... Clearly $$A\leq f(t) \leq B$$ since $$f$$ is increasing ... ... "
Can someone demonstrate, formally and rigorously that $$A\leq f(t) \leq B$$ ... ...Note: Although it seems highly plausible, given the definitions of $$A$$ and $$B$$ and given also that $$f$$ is increasing, that $$A\leq f(t) \leq B$$ .. I am unable to prove it rigorously ... Hope someone can help ...

Peter

 

[GJA]

Hi Peter,

Since $f$ is increasing we know $x_{1}<x_{2}\,\Longrightarrow\, f(x_{1})\leq f(x_{2}).$ This means that $f(t)$ is an upper bound for the set $\{f(s)\,\vert\, s < t\}$ and a lower bound for $\{f(s)\,\vert\, t<s\}$. Does that help resolve the issue?

 

[Math Amateur]

Hi Peter,

Since $f$ is increasing we know $x_{1}<x_{2}\,\Longrightarrow\, f(x_{1})\leq f(x_{2}).$ This means that $f(t)$ is an upper bound for the set $\{f(s)\,\vert\, s < t\}$ and a lower bound for $\{f(s)\,\vert\, t<s\}$. Does that help resolve the issue?

Thanks so so much for the help GJA ...

Reflecting on what you have said ...

Beginning to suspect that I'm overthinking this issue ...

Thanks again for the help ...

Peter

 

[GJA]

Hi Peter,

Always happy to help in any way that I can. I had a tough time too when it came to understanding supremums and infimums. The words "least upper" and "greatest lower" don't hit the ear right initially.