Inductance of a Solenoid with a Core inside

[titansarus]

Homework Statement

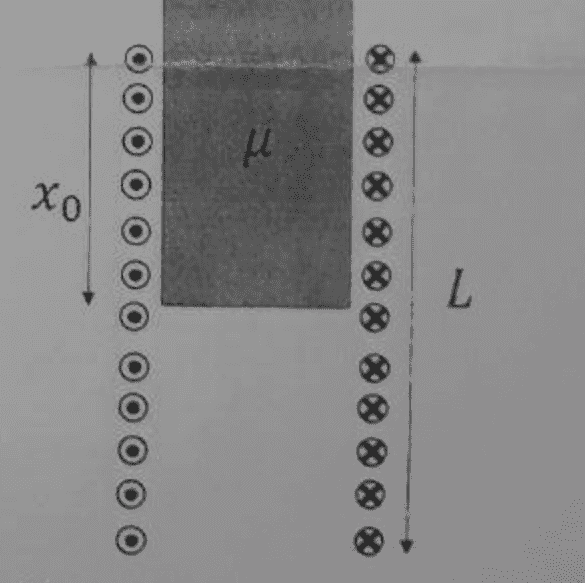
We have an Ideal Solenoid with current $I$ and turn per length $n$ and a core with magnetic permittivity of $\mu$ is inside it like the figure. the length $x_0$ of solenoid has the core and the rest is empty. Find the Inductance of a Solenoid.

Relevant Equations

$\int B ds = \mu I$, $L_T = L_1 + L_2$

The question said the $\mu$ in question is the $\mu$ in the above equation so no need to worry about scale factor.

For finding magnetic field $B$, We see this question like two Solenoids. for the first one, we have $\int B ds = \mu I$ so $B x_0 = \mu I n x_0$ so $B = \mu n I$. For the second one we have $B = \mu_0 n I$. For the Inductance we have $L = \mu l n^2 A$ so we have $L_1 = \mu x_0 n^2 A$ and for the second one we have $L_2 = \mu_0 (L-x_0) n^2 A$. And the $L_{total} = L_1 + L_2$

Is my reasoning right? I think I didn't considered mutual Inductance but the question is from an exam and it was orally said you don't need to consider mutual inductance.

 

[rude man]

Ignoring mutual inductance makes no sense. The inductance for any solenoid is approximately calculated assuming full coupling between each winding. That's where all those n^2 and N^2 terms come from. Why should it be different for the same solenoid except part of it has a slug inside?

I would approach this from an energy viewpoint. Very straightforward that way.

 

[titansarus]

Ignoring mutual inductance makes no sense. The inductance for any solenoid is approximately calculated assuming full coupling between each winding. That's where all those n^2 and N^2 terms come from. Why should it be different for the same solenoid except part of it has a slug inside?

I would approach this from an energy viewpoint. Very straightforward that way.

I don't know how to solve this with energy? How is that? I just know energy is $\frac{1}{2} L i^2$. But I don't know how to use this the calculate inductance in this question.

 

[rude man]

I don't know how to solve this with energy? How is that? I just know energy is $\frac{1}{2} L i^2$. But I don't know how to use this the calculate inductance in this question.

You're off to a good start. Now, what are the B fields in both parts of the solenoid, and then the energies of the B fields in both parts of the solenoid?

BTW were you given the cross-sectional area of the solenoid? You need that parameter.

 

[titansarus]

You're off to a good start. Now, what are the B fields in both parts of the solenoid, and then the energies of the B fields in both parts of the solenoid?

BTW were you given the cross-sectional area of the solenoid? You need that parameter.

I will get $B$ as $B_{with~ core} = \mu n I$ and $B_{without~core} = \mu_0 n I$, Right? And the energy of $B$ field is $\frac{1}{2}\frac{B^2}{\mu}$ where $\mu$ is the magnetic permittivity of that region of space. is this Right? Should I say that sum of these two energies of $B$ fields equals $\frac{1}{2} L i^2$ where $L$ is the equivalent induction?

For the cross-section area, The area of Core and Solenoid are both equal to $A$. (The core completely fits into the solenoid)

 

[rude man]

Is 1/2 BH = 1/2 B^2/μ energy or energy density?
BTW you can help me too. How did you manage to write B^2 the right way, i.e. B superscript 2?

 

[titansarus]

Is 1/2 BH = 1/2 B^2/μ energy or energy density?
BTW you can help me too. How did you manage to write B^2 the right way, i.e. B superscript 2?

I think i was wrong. $\frac{1}{2} \frac{B^2}{ \mu}$ is energy density. I think I must multiply it by $A * x$ for the part that has the core and by $A * (L-x)$ for the part that hasn't. Beside this, Is my way correct.

For the subscript and superscript and actually any formula, you must write the formula between two #. Like this picture:

$\int_0^\infty \mu_1^2 \frac{1}{2} dx$

 

[rude man]

I think i was wrong. $\frac{1}{2} \frac{B^2}{ \mu}$ is energy density. I think I must multiply it by $A * x$ for the part that has the core and by $A * (L-x)$ for the part that hasn't. Beside this, Is my way correct.

For the subscript and superscript and actually any formula, you must write the formula between two #. Like this picture:

$\int_0^\infty \mu_1^2 \frac{1}{2} dx$View attachment 245286

Right! You're there!

I'm familiar (sort of) with LaTex so OK now I know. Before the latest console revision you could write subscripts and superscripts without resorting to LaTex. Thx.