gillouche
Gold Member
- 25
- 7
Hi,
I have some troubles to understand the next step for the solution. If you need more informations, please let me know.
1. Homework Statement
A moving vehicle of mass M is moving down an inclined plane of angle alpha with respect to the horizontal plane. What is the force indicated on the scale ?
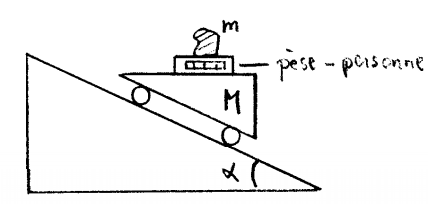
It is written pèse-personne between M and m. That's a scale (to weight people)
[/B]
Acceleration of M on the inclined plane : a = g*sin(alpha) * (M/m + 1)
[/B]
I started to try to find the acceleration of M on the inclined plane. I have the following forces acting on my moving vehicle : gravity (down), normal force (perpendicular to the inclined plane) and the weight of the mass m (it is not indicated but I assume that the scale doesn't have a mass).
I separated the gravity components in parallel and perpendicular component and I get :
Fg parallel inclined plane = (M+m)g * sin(alpha)
The Fg perpendicular cancels out with normal force. I don't think I need it but that's the same of Fg parllel but with cosine.
Then I have ma = (M+m)g * sin(alpha) which gives me a = g*sin(alpha) * (M/m + 1)
(I can give the steps if needed).
Now I am stuck. How can I find the normal force for m ?
For m, I have the weight (down), the normal force (up), acceleration (right) and inertia (left). Those orientations are with respect to the moving vehicle and not the inclined plane. Am I supposed to break all the components in their parallel and perpendicular (to the inclined plane) components ?
I am confused with this inclined and not inclined plane of the moving vehicle. The exercises we did before was an elevator (for the weight) and a moving vehicle on the horizontal axis (to introduce inertia).
Thanks.
I have some troubles to understand the next step for the solution. If you need more informations, please let me know.
1. Homework Statement
A moving vehicle of mass M is moving down an inclined plane of angle alpha with respect to the horizontal plane. What is the force indicated on the scale ?
It is written pèse-personne between M and m. That's a scale (to weight people)
Homework Equations
[/B]
Acceleration of M on the inclined plane : a = g*sin(alpha) * (M/m + 1)
The Attempt at a Solution
[/B]
I started to try to find the acceleration of M on the inclined plane. I have the following forces acting on my moving vehicle : gravity (down), normal force (perpendicular to the inclined plane) and the weight of the mass m (it is not indicated but I assume that the scale doesn't have a mass).
I separated the gravity components in parallel and perpendicular component and I get :
Fg parallel inclined plane = (M+m)g * sin(alpha)
The Fg perpendicular cancels out with normal force. I don't think I need it but that's the same of Fg parllel but with cosine.
Then I have ma = (M+m)g * sin(alpha) which gives me a = g*sin(alpha) * (M/m + 1)
(I can give the steps if needed).
Now I am stuck. How can I find the normal force for m ?
For m, I have the weight (down), the normal force (up), acceleration (right) and inertia (left). Those orientations are with respect to the moving vehicle and not the inclined plane. Am I supposed to break all the components in their parallel and perpendicular (to the inclined plane) components ?
I am confused with this inclined and not inclined plane of the moving vehicle. The exercises we did before was an elevator (for the weight) and a moving vehicle on the horizontal axis (to introduce inertia).
Thanks.