JJNic
- 4
- 0
I have a question regarding the exact formulation of the mechanism of Inflation.
In thehttp://www.damtp.cam.ac.uk/user/db275/Cosmology/Lectures.pdf he uses ##\frac{d}{dt} \frac{1}{aH} < 0## as an definition of inflation. I see that it yields ## \ddot a > 0##, but my confusion lies in the interplay between the particle horizon and the comoving Hubble radius.
Why do we require ## \frac{1}{aH} \ll \chi_p## in the early universe? He says
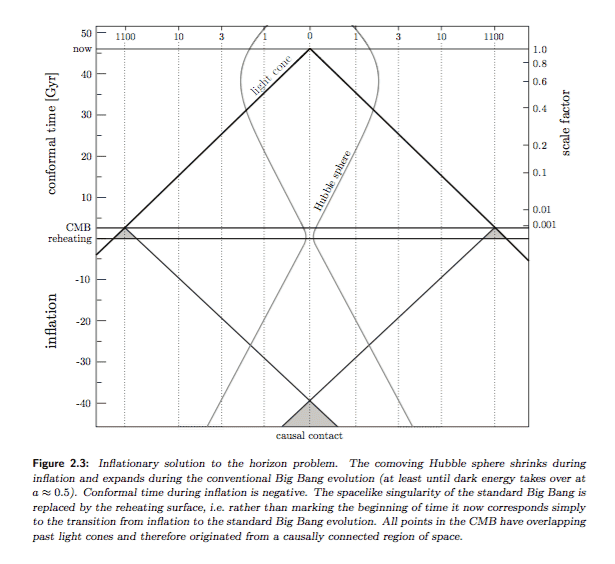
I see that the horizon problem gets solved because the points p and q now have overlapping particle horizons, but what does the comoving Hubble sphere have to do with it?
They would still have overlapping particle horizons if i did not draw the Hubble sphere or if i drew it differently. Or is it not possible to have both things at the same time? (a different Hubble sphere AND overlapping particle horizons of p and q).
To me it just seems that "adding more conformal time before the initial singularity and shift it to -inf. or less" s.t. p and q have overlapping particle horizons would do the job just fine, not worrying about the comoving Hubble radius.So, i am obviously missing something, but what is it?
Thanks!
In thehttp://www.damtp.cam.ac.uk/user/db275/Cosmology/Lectures.pdf he uses ##\frac{d}{dt} \frac{1}{aH} < 0## as an definition of inflation. I see that it yields ## \ddot a > 0##, but my confusion lies in the interplay between the particle horizon and the comoving Hubble radius.
Why do we require ## \frac{1}{aH} \ll \chi_p## in the early universe? He says
But i don't see how that goes about.I am especially confused by figure 2.3 on page 33 (i cropped and attached it for your convenience),This means that particles can’t communicate now (or when the CMB was created), but were in causal contact early on.
I see that the horizon problem gets solved because the points p and q now have overlapping particle horizons, but what does the comoving Hubble sphere have to do with it?
They would still have overlapping particle horizons if i did not draw the Hubble sphere or if i drew it differently. Or is it not possible to have both things at the same time? (a different Hubble sphere AND overlapping particle horizons of p and q).
To me it just seems that "adding more conformal time before the initial singularity and shift it to -inf. or less" s.t. p and q have overlapping particle horizons would do the job just fine, not worrying about the comoving Hubble radius.So, i am obviously missing something, but what is it?
Thanks!