lievbirman
- 4
- 0
Hello all,As an exercise my research mentor assigned me to solve the following set of equations for the constants a, b, and c at the bottom. The function f(r) should be a basis function for a cylindrical geometry with boundary conditions such that the value of J is 0 at the ends of the cylinder.
I'm having trouble finding textbooks with the information I must know to solve these equations. If anyone can point me in the right direction I would be very grateful. From what I understand thus far, the functions should be some variant of Bessel functions, and this method is that of basis functions.
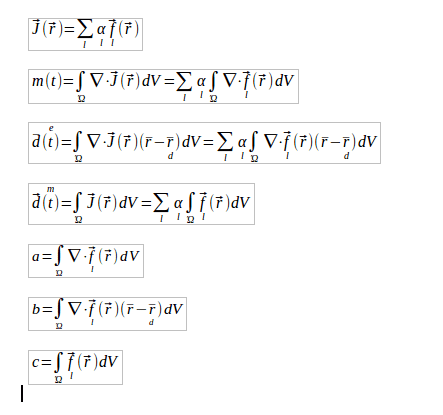
I'm having trouble finding textbooks with the information I must know to solve these equations. If anyone can point me in the right direction I would be very grateful. From what I understand thus far, the functions should be some variant of Bessel functions, and this method is that of basis functions.