Solving Special Function Equations Using Lie Symmetries

[bolbteppa]

The lie groups + representation theory approach to special functions & how they solve the ode's arising in physics is absolutely amazing. I've given an example of it's power below on Bessel's equation.

Would anyone have a non-dense/explicit/easy reference aimed at physicists for the relationship between the special functions of mathematical physics, lie groups and representation theory? Something paralleling my example of Bessel's equation. Or maybe we could use this thread to post geometric explanations of all these ode's!

The standard references are Miller & Vilenkin, but they are far too dense, too much unnecessary information for my purposes & I have no idea/time how to sift through it all. I'd really like a short, direct exposition of this material as it relates to the special functions you get from separating the Laplacian like the Hypergeometric, Legendre, Bessel, Airy etc... equations in a geometric way, if such a thing exists. I believe it's something like a geometric interpretation of Weisner's method.

For example, Bessel's equation seems to be saying, find a function in the plane such that when we shift it right, then shift it back left again, all locally (i.e. differentially), we get the same function:

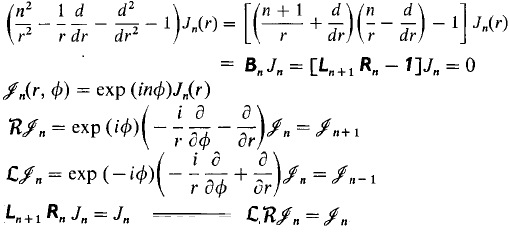
(c.f. Killingbeck, Mathematical Technique's and Applications, sec. 8.21).

The idea is to take Bessel's equation, factor it, add an extra variable to make the factors parameter independent so that they become elements of a lie algebra, identify the meaning of those factors, in this case notice the Lie algebra factors are translations in Polar coordinates, and realize it's just a differential expression of a symmetry.

Bessel's equation arises from $LRv = v$ when you express $L$ & $R$ in polar coordinates. It makes sense to express them in polar coordinates since Bessel arises from separating the Laplacian assuming cylindrical symmetry, and the $LRv = v$ assumption (not $LRv = w$) is motivated by the symmetry of the Laplacian.

Using this idea we can, for some reason, actually solve Bessel's equation with a picture!:

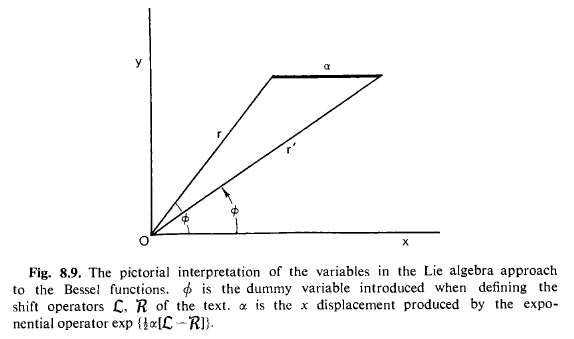We just want to shift $\mathcal{J}_n(r,\phi)$ in the x-direction using the operator $e^{a\tfrac{\partial}{\partial x}}$ expressed in polar coordinates: $e^{\tfrac{a}{2}(\mathcal{L}-\mathcal{R})}$ and realize it will be equal to $\mathcal{J}_n(r',\phi')$:

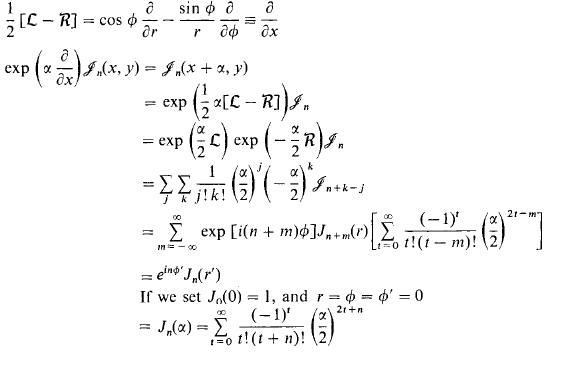So the last line comes from dragging all this to the origin and putting it along the x-axis, here we see the geometric meaning of Bessel functions!

Hypergeometric is supposed to be related to $SL(2,R)$ symmetries, Bessel to translational planar symmetries, the Gamma function related to linear symmetries $y = ax + b$, etc... Is there an easy unified geometric exposition on how to deal with these babies?

References:

1. Killingbeck, Mathematical Technique's and Applications, sec. 8.21
2. Vilenkin, Representation of Lie Groups and Special Functions Vol. 1
3. Vilenkin, Special Functions and Theory of Group Representations
4. Miller, Lie Theory and Special Functions
5. Kaufman, Special Functions of Mathematical Physics from the Viewpoint of Lie
Algebra

 

[ellipsis]

I'm interested in this, but I don't know near enough math to know what the implications are. What are Bessel functions used for in physics?

 

[JJacquelin]

Hi !
I posted a comment on the "conversation" forum : https://www.physicsforums.com/conversations/special-functions.12420/

@ ellipsis : somme physical applications are listed here :
http://en.wikipedia.org/wiki/Bessel_function

The topic is also related to the more general question of classifying and naming the special functions : https://www.physicsforums.com/threads/remembering-special-function-equations.717354/
which subject is mentioned in : https://fr.scribd.com/doc/14623310/Safari-on-the-country-of-the-Special-Functions-Safari-au-pays-des-fonctions-speciales

 

[Strum]

Hallo!

Unfortunately I can't help you with anything besides acknowledging that this is a really nice topic:). Did I miss something in the conversation forum? I doesn't seem to work anymore.
Quick question. In the first picture how do you find $\mathcal{R}$ and $\mathcal{L}$? It easy to see that it works, but are there some general methods to split up a large operator into smaller commutative operators? Exponentiation can be somewhat hard to figure out otherwise.

 

[bolbteppa]

I don't know, I'd love to know a good answer to that, the Kaufman article basically takes Bessel, Legendre, Associated Legendre, Gegenbauer, Chebyshev & Hermite and decomposes them all into this left-right invariance by postulating those decompositions in advance, I think it's from factoring the equations and noticing it represents differential operators in some special coordinate system, which syncs with the notion of these equations arising out of the Laplacian in certain coordinates (page 8). I'd like to write up a fool proof system of dealing with all the standard equations in Whittaker-Watson and arising from the Laplacian at least with this method. If you look in Vilenkin's 3 volume work he seems to show this method does include functions like elliptic functions and other special functions, so it's pretty general.

If you guys find something nice for any of the other equations, even half-attempts, just post them here and we can build on them!

 

[DarthMatter]

Please let me ask a possibly dumb/basic question. Why isn't it true that shifting a function left and right again (differentially) results in the same function for all functions? Does this have to do with the chosen coordinate system?

 

[Stephen Tashi]

I haven't read bolbteppa's example, but in the general case, shifting depends on the choice of coordinate systems. I'm reading this simple explanation now: http://euler.nmt.edu/~jstarret/05-649LieGroupODEFinalVersion.pdf