kurosama
- 2
- 0
- TL;DR
- I have a system that seems to suggest that it may possible to transfer information at much greater speeds than light. This seems completely ridiculous and I am definitely missing an important factor in my speculations/calculations. I need help understanding this phenomenon and where am I going wrong in this thought experiment.
Let us consider a hypothetical scenario, where we are able to translate any mass at a constant speed of 10m/s w.r.t to a given frame of reference. For simplicity, we are going to assume that the object is at rest initially.
Case 1 -
Now, consider 2 points A and B at a distance of 10m, and our goal is to transport some information from point A to point B in 1s. Now, this is a trivial case, in this case, we can simply send a point mass M at the constant speed of 10m/s and achieve the goal.
Case 2 -
Now, let's suppose points A and B are 20m apart, and our goal is again to transport the information in 1s. In this case, we can create a 10m long trailer starting at A, now we move the trailer at 10m/s, and place the point mass inside the trailer, and move the point mass at 10m/s wrt to the trailer, so in this case the front of the trailer covers 10m in 1s, the point mass covers the distance inside the trailer in 1s and reaches it's front. So effectively, we were able to cover 20m in 1s.
Case 3 -
Now, similarly, assume, A and B were at 30m. In this case, we can initially place a 20m long trailer, and then a 10m long trailer inside of it, and then the point mass inside of it, the outermost trailer moves at 10m/s w.r.t the observer outside, the inner trailer moves at 10m/s wrt to the outermost trailer, the point mass moves at 10m/s w.r.t the innermost trailer, so we are able to cover 30m in 1s with the point mass.
Now, similarly carrying on for extremely large distances (please refer to the image), this framework seems to suggest that any arbitrary distance can be covered in just 1s without any cosmic limits affecting it. Of course, the setting is hypothetical and practically it may never be possible to achieve such a mechanic.
This mechanics is causing a lot of confusion and I am unable to figure out what's wrong with my calculations. Of course, the scenario is completely hypothetical, but I believe imposing natural boundaries that we can never build such machinery shouldn't stop us from speculating a possible observation if it were to exist. This model suggests that the information the point mass is carrying is traveling faster than light which should not be possible. I am not really concerned with the relative speed of the innermost trailer wrt to an observer on A, but rather being mostly confused about the fact that how is such a large distance covered in just 1s. Case 1, 2, 3 are not so fictional and we can see this happening in real life as well. So how is it that just by increasing the number of outer trailers I am bounded by space and time to not exceed the speed of light wrt someone else?
PS: I am not sure if the question is a repeat of someone proposing a similar scenario, I am new to the forum and couldn't find anything similar to the scenario that I am looking for, and it was incredibly hard to find material on what's going on with the distances!
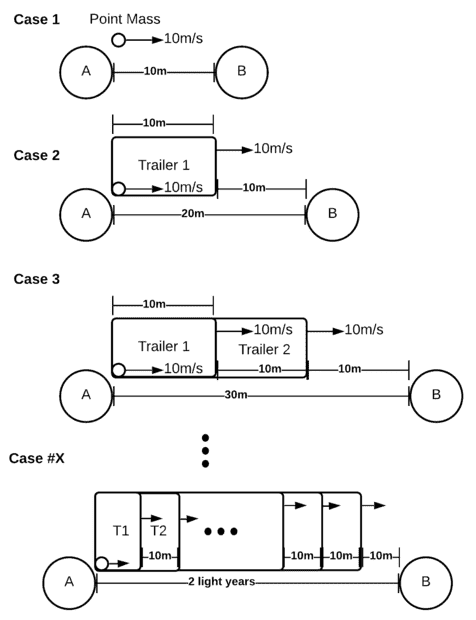
Case 1 -
Now, consider 2 points A and B at a distance of 10m, and our goal is to transport some information from point A to point B in 1s. Now, this is a trivial case, in this case, we can simply send a point mass M at the constant speed of 10m/s and achieve the goal.
Case 2 -
Now, let's suppose points A and B are 20m apart, and our goal is again to transport the information in 1s. In this case, we can create a 10m long trailer starting at A, now we move the trailer at 10m/s, and place the point mass inside the trailer, and move the point mass at 10m/s wrt to the trailer, so in this case the front of the trailer covers 10m in 1s, the point mass covers the distance inside the trailer in 1s and reaches it's front. So effectively, we were able to cover 20m in 1s.
Case 3 -
Now, similarly, assume, A and B were at 30m. In this case, we can initially place a 20m long trailer, and then a 10m long trailer inside of it, and then the point mass inside of it, the outermost trailer moves at 10m/s w.r.t the observer outside, the inner trailer moves at 10m/s wrt to the outermost trailer, the point mass moves at 10m/s w.r.t the innermost trailer, so we are able to cover 30m in 1s with the point mass.
Now, similarly carrying on for extremely large distances (please refer to the image), this framework seems to suggest that any arbitrary distance can be covered in just 1s without any cosmic limits affecting it. Of course, the setting is hypothetical and practically it may never be possible to achieve such a mechanic.
This mechanics is causing a lot of confusion and I am unable to figure out what's wrong with my calculations. Of course, the scenario is completely hypothetical, but I believe imposing natural boundaries that we can never build such machinery shouldn't stop us from speculating a possible observation if it were to exist. This model suggests that the information the point mass is carrying is traveling faster than light which should not be possible. I am not really concerned with the relative speed of the innermost trailer wrt to an observer on A, but rather being mostly confused about the fact that how is such a large distance covered in just 1s. Case 1, 2, 3 are not so fictional and we can see this happening in real life as well. So how is it that just by increasing the number of outer trailers I am bounded by space and time to not exceed the speed of light wrt someone else?
PS: I am not sure if the question is a repeat of someone proposing a similar scenario, I am new to the forum and couldn't find anything similar to the scenario that I am looking for, and it was incredibly hard to find material on what's going on with the distances!