RuthlessTB
- 22
- 0
I started recently to study physics for motions, it is interesting so far but sadly I need some basic knowledge in calculus, I can get the Instantaneous velocity if the question gave me a function of time, but I don't know how to get it from a graph.
I used the equation of calculating average velocity but I think it is wrong.
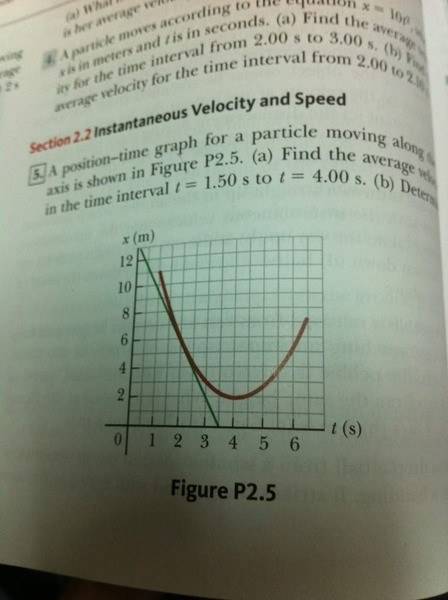
Can somebody explain to me how to calculate Instantaneous velocity from a graph?
I attached a picture, so someone can explain to me.
I used the equation of calculating average velocity but I think it is wrong.
Can somebody explain to me how to calculate Instantaneous velocity from a graph?
I attached a picture, so someone can explain to me.