Integrals are harder than derivatives, why?

[mathwonk]

this is for @wolly , in particular the question in post #30.
sorry for the confusion. i forgot that in many elementary books the word "integrate" is used as a synonym for the word "antidifferentiate", and "integral" is equated with "antiderivative". this in my opinion is very harmful to the student. the reason of course for this practice is the theorem that if a function f is continuous, then its integral, in the correct sense of a limit of sums, is a differentiable function of the upper limit, and that derivative is f. An integral however is by definition a limit of sums, and the antiderivative is merely a tool, or trick, for calculating it. For this reason, we all start out early using only this trick and forgetting largely the definition of the integral as a limit. The one exception is the excellent book of Apostol where integrals are treated first and at length, before introducing the derivative and its use in computing integrals.

The harm comes for several reasons. First of all, the theorem has a hypothesis, continuity of f. So what do we do when f is not continuous?. In that case the integral may not be differentiable as a function of the upper limit. E.g. it is a basic theorem following from the mean value theorem that if f is a derivative, then it has the intermediate value property. In particular a step function is not a derivative, hence its integral is not an antiderivative, at least not in the usual sense, but the integral of a step function is easily computed using sums. Thus the most basic Riemann sums used to approximate integrals, although certainly integrable, are not themselves directly antidifferentiable.

This problem raises its head again in complex variables, where again one defines path integrals in terms of limits of sums, and then proceeds to prove many fundamental theorems like the Cauchy integral theorem and residue theorem, which may be lost on most students who think of integrals merely in terms of antiderivatives. I.e. in complex variables most integrands do not have antiderivatives, or else all path integrals would equal zero. E.g. the first interesting integral one meets is that of dz/z taken around the unit circle. One wants the antiderivative to equal the logarithm but there is no way to define the log function on any set containing the unit circle. This same situation comes up in vector calculus, since most differentials are not exact, and even closed differentials are exact only locally. indeed dz/z is a closed, locally exact, differential that is not exact on any neighborhood of the origin. The problem of course is that given a (starting point p and a) point q, the antiderivative can only make sense if it has a unique value at q, whereas the path integral is defined in terms of a path from p to q. The integral makes sense for all paths, but the antiderivative only makes sense if the values for all choices of paths are the same. I think now this is why my complex class just stared uncomprehendingly, throughout the discussion of path integrals and their properties. The word "integral" may have just had no meaning for them without the crutch of antiderivatives.

Another matter, which really is at the heart of the question here I think, is that differentiation is an operation that strictly shrinks the class of functions one is working on, i.e. it takes functions and tends to make them more elementary. Thus a very abstract and sophisticated function, like the logarithm, can have a very elementary looking function like 1/x. This makes it hard to go backwards, since the antiderivative of an easy function tends to be more difficult, or more abstract. Indeed according to the fundamental theorem quoted above, the only reason we believe that a continuous function should have an antiderivative is that one can be constructed, or at least approximated, by its limiting sums. Thus this direction, starting from the integral as a limit of sums, and using that to try to find an antiderivative, is the only direction that will always work. I.e. trying to work backwards, and just guess or somehow cook up an antiderivative, and use that to compute an integral, will only work in special very easy cases.

oh yes, the presence of the C that is worrying the student comes from the theorem that the derivative of a constant C is zero, so the antiderivative of zero is only pinned down at best to being some constant C. Thus for any continuous function f, since f = f+0, its antiderivative can only be pinned down to within a constant C. I.e. if g is one antiderivative, then g+C is another one for every constant C.

Notice this only applies to continuous functions, so e.g. if a book claims that the general antiderivative of 1/x is ln(|x|) +C, this is wrong, since 1/x is not continuous. I.e.
we could take ln(|x|) + C1 for x<0, and ln(|x|) +C2, for x>0, where C1 and C2 are different constants.
Note too that in the complex domain this C is what saves you in some cases. I.e. for the various different choices of a logarithm on the punctured plane, any 2 differ by a constant, so they all have the same derivative! Thus even though the antiderivative is not well defined, its derivative is! Or backwards, even though the integrand is well defined, hence also its (path) integral, nonetheless the antiderivative may not be.

so this is roughly what i was thinking of, and i hope it helps someone, apologies if it does not.Remark: If you are aware of Lebesgue integration you know that continuity of the integrand can be dispensed with at the cost of dealing with functions which are differentiable almost everywhere. e.g. in the case of the step functions, we can "antidifferentiate them" by using piecewise linear functions, in the sense that a suitable piecewise linear function is continuous, and has a derivative at all but a finite set of points, where it is still continuous, and at all other points it is differentiable and its derivative equals the step function. Such an "almost everywhere" antiderivative can then be used to compute the (definite) integral of a step function. For example, the absolute value function is a good antiderivative of the function that equals -1 for negative x and +1 for positive x, and anything at x=0. (We don't care about the value at zero since it cannot affect the value of the integral.) I.e. that step function has a definite integral on any interval and the absolute value function can be used to calculate it. But the point again is that one really uses here the definition of the integral as a limit of sums to find the antiderivative, not the other way around.Svein's post too is very interesting, to me especially the point that the integral is a "smoothing operation".

As some of you probably know, integrals can even be used to define derivatives of functions that are not differentiable in the usual sense anywhere! i.e. if f is any locally integrable function, then it acts on smooth (infinitely differentiable) compactly supported functions g by integrating their product fg. And integration is so sensitive that knowing these integrals for all g determines f almost everywhere. So even if f is nowhere differentiable in the usual sense, we can still determine what Df should be by telling what its value on every smooth compactly supported g is. For by the formula for integration by parts, we should have that the integral of gDf + fDg should be zero (since g and hence Dg are suported on a finite interval), hence we can define the integral of gDf to be minus the integral of fDg. This is called the "distribution derivative" of f. We don't get it immediately as a function, but we do know how a function representing it should act on all smooth (compactly supported) functions. This is useful even in the case of functions f that do have a derivative, in fact one can solve some differential equations in two stages, first by finding the distribution derivative or distribution solution, and then proving that solution is actually represented by a function.

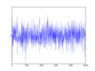
Note that the basis for this use of integrals to define derivatives is that precisely the opposite of the original complaint is true, i.e. integrals are far easier, at least theoretically, than derivatives, e.g. far larger classes of functions can be integrated than can be differentiated, and as Svein observed, the integrals have better properties. E.g. a locally integrable function has of course an integral by definition, even though it may be very rough or noisy, but it takes this very clever stratagem to even begin to define its derivative.

I will try now to stop adding to this very pregnant discussion topic. But I suggest for wolly, that a perusal, or better, a careful study, of the first part of Apostol, where he does integrals before derivatives, could be very instructive, since you seem to seek understanding as opposed to memorizing.

 

[mathwonk]

can't resist one more example of why integrals are "easier than" derivatives. in fact among all continuous functions, most of them do not have derivatives anywhere, but they all have integrals, and it is easy to approximate the values of those integrals by estimating them by step functions. hence most are "easy to integrate" but impossible to differentiate. the most famous example, due to weierstrass, was even given as a Fourier series, in fact as a limit of just cosines:

https://en.wikipedia.org/wiki/Weierstrass_function

Note too that since this function is continuous, hence locally integrable, it does have a "distribution derivative", in the sense that it operates on smooth compactly supported functions.

 

[mathwonk]

to elaborate the basic idea of symbolipoint's post: recall that subtraction is defined in terms of addition, i.e. a-b is defined as that number c such that b+c = a. similarly a/b is defined as that number c such that bc = a, and the antiderivative of f is defined as that function g such that g' = f, etc... this means that to calculate a-b from the definition, you have to add all possible number to b and wait until you get a as an answer, and similarly in the other cases. it is amazing when there is any procedure at all that helps find the "opposite" of an operation. that's why solving equations is hard. these tiny examples amount to solving the equations bx = a, or b+x = a, or y' = f ...

If anyone takes the time to process these posts I will enjoy any feedback. the main point is that although it is nice to use an antiderivative to compute an integral, in general this is impossible and the only way to find most antiderivatives is to use an integral, i.e. a "definite" integral, or limit of sums, but computed with a variable upper limit. moreover, most functions can be integrated but not differentiated, and even for almost all elementary functions that one can write down, the antiderivative given by the integral, is a totally unfamiliar function you cannot write down any other way than as a limit of sums, and have never seen before or heard of.

Just for fun, you know the absolute value function is continuous, so it must have an antiderivative. Can you write it down? Hint: it's not hard, and you can work on one side of the y-axis at a time. Just make sure your final answer is continuous.

 

[WWGD]

Well can someone prove that integrals are not antiderivatives?Please explain!

EDIT I don't know if this is what you are looking for, but there is, e.g., the Volterra function V , which is everywhere differentiable but $\int V' \neq V$ . Maybe the concept that comes into play here is absolute continuity. I think a standard example is that of the Cantor function C which has the same property. Since C is a.e. 0 , C'=0 a.e., but , as with the Volterra function V $\int C' \neq C$ ; but V' is not even integrable , so we do not always recover the function as the integral of the derivative , so these terms are not , strictly -speaking, inverses of each other. EDIT: What I mean is that , only within the class of absolutely continuous functions, the two operations are inverses of each other.

 

[mathwonk]

these are very nice and illustrative examples. they may be examples of the logically opposite statement however, since they are examples of antiderivatives that are not integrals. in all cases of lebesgue integrable functions f, the integral of f is an antiderivative (almost everywhere) of f, by lebesgue's theorem. of course it depends on your definition of antiderivative. i.e. even in the riemann case, unless f is continuous, it is not necessarily true that an integral is an everywhere differentiable antiderivative. but for every reimann integrable f, it is a (Lipschitz continuous, hence also absolutely continuous) function which is a differentiable antiderivative of f almost everywhere.

obviously this is a somewhat complicated topic, and i am not an expert, i.e. i am a geometer and not an analyst.

but from the combination of the posts of WWGD and these remarks, it seems that using lebesgue integration, every (lebesgue) integral is an antiderivative (a.e.), but some antiderivatives are not integrals, only absolutely continuous ones are. thank you WWGD, this clarifies things at least for me. In particular, integrals are not the same thing as antiderivatives. I.e. an integrable function can have many antiderivatives, but only those which are also absolutely continuous can occur as integrals.

His Cantor example shows this, since it is a con tinuous (but not absolutely continuous) antiderivative of the zero function. The only integral however of the zero function is the zero function. To put it another way, among all the antiderivatives of an integrable function, the integral picks out the unique (up to a constant) absolutely continuous one. The key lemma is the one that in the classical case follows from the mean value theorem: if a continuous function has derivative zero almost everywhere, is it a constant? The answer is not necessarily, unless the function is also absolutely continuous.

To @wolly, this relates to your question about the constant C. I.e. if you define an antiderivative of f as a function that is differentiable everywhere and the derivative equals f everywhere, then any two differ by a constant C. But if we define an antiderivative of f as a continuous function with derivative almost everywhere equal to f, then two of these can differ by a function like the Cantor function! I.e. it is n ot necessarily a constant but it does have derivative zero almost everywhere, But if we define an antiderivative as an absolutey continuous function whose derivative equals f almost everywhere then any two of these do differ by a constant C.

In the Riemann case it is harder to provide inverse operations. I.e. every riemann differentiable function f is continuous almost everywhere, and its integral is lipschitz continuous and differentiable everywhere f was continuous, hence almost everyhere, and the value of that derivative equals f almost everywhere. But if we start with a lipschitz continuous function g which is also differentiable a.e. (in fact that is guaranteed) , then it is not always true that its derivative g' is riemann integrable, although it will be lebesgue integrable, with lebesgue integral equal to g + C, for some constant C. So in the riemann case we do not even know a condition that guarantees a function is the integral of some riemann integrable function, i.e. lipschitz continuity is necessary but apparently not sufficient. in the lebesgue case, we do know that every absolutely continuous function is the integral of its derivative, hence is an integral and an antiderivative.

since I am not an expert, i recommend reading a book by an analyst like Sterling Berberian, on integration and measure theory, or for the ambitious, the book Functional Analysis, by Riesz-Nagy.

 

[mathwonk]

by the way, it is not expected that someone with a basic question on this can understand all this fairly sophisticated stuff that has been posted. it is only meant as an attempt to provoke discussion. all and any questions on any aspect of it are welcome. so just take a sentence or two, process them and ask away.

my goal i achieved if someone has been given more examples to think more about whether an integral is or is not the same as an antiderivative, and what that question means, which is the same as the OP's question in #30.

 

[Aufbauwerk 2045]

Just to follow up on what I said earlier about integration, it may help to understand it from a computational viewpoint. It's actually amazingly simple in that sense.

Here is a reference from my library which is a bit dated but still quite useful. "BASIC Programs for Scientists and Engineers" by Alan Miller. It's a very easy introduction to many useful topics, including numerical integration. (To be followed up perhaps by those who need it with the classic Numerical Recipes in C (or if you must C++) by Press et al.)

Miller provides three different ways of computing the integral, using just 27 pages (Ch. 9) . Compare the simplicity of writing a program to do numerical integration with a program to solve partial differential equations!

In general, I've found that programming something, or at least learning how it's done, makes some things much clearer. This is especially true when you are writing the program, because, as the saying goes, you really understand something when you can tell a computer how to do it.

 

[Svein]

Going from mathematics to physics (electronics) - here is an integrator:

This integrator has a frequency response like this:

You can also create a differentiator:

The frequency response of such a circuit is something like this:

 

[WWGD]

by the way, it is not expected that someone with a basic question on this can understand all this fairly sophisticated stuff that has been posted. it is only meant as an attempt to provoke discussion. all and any questions on any aspect of it are welcome. so just take a sentence or two, process them and ask away.

.

That is my usual approach: to answer the big questions, start early. You will likely not understand it the first time around , but you will start breaking it down in the back of your mind. But I have been chided here by some moderators for this. They seem to think I am too over the top .

 

[mathwonk]

the best professors i have had have answered questions in a way i have not understood sometimes for years. they really give you a lot, but you have to make an effort.

 

[Dr. Courtney]

I didn't really understand these subtleties until a couple years after my first calculus sequence. Applications in physics helped, but what helped the most was when I finally got to a numerical analysis course and learned how to compute just about any derivative or integral numerically (and also how to integrate differential equations numerically. Somehow the computational approach (as opposed to the pencil and paper analytical approach) was the missing piece for my conceptual understanding.

 

[votingmachine]

I understand the concept of derivatives but when it comes to integrals and their uses I do not understand what they do and where you use them.In derivatives you can understand how a function changes but in integration everything is so illogical.Can someone explain me the use of integrals in calculus?I mean all I could understand is that there is some +C which is a constant but I have no idea where that come from.What does this +C even mean?When I look at derivatives I can see that the function changes but when I look at a integral I have no idea what a function does in that specific function.All I know is that I learned(more memorized) and I couldn't understand the complexity of them.
I have a math book full of exercises and it doesn't explain at all how a integral works.It just shows me some integrals that I learned in high school and most of them don't even show the proof behind them.

Two examples might clear it up.

Say you know you are filling a tank at 1 gallon per minute. How much water do you have after 15 minutes? You have added 15 gallons to the tank +C, the amount that was in the tank.

Say you are traveling West at 10 miles per hour. How far West of Washington are you after 15 hours? You have traveled 150 miles west, +C, the miles west of Washington you started.

In both cases it was a dx/dt = k. Integrating let's you quantify the total, but only if you know that starting condition C.

I integrate times and distances in my head when I drive. But I use my assumed average speed. If I'm 60 miles from home and expect to drive at 40 mph on average, I know I'll be home in an hour and a half. I have integrated my velocity function.
v=dx/dt=40 miles per hour
x= integral of dx/dt = 40t + C.
And I know C is 0 miles and x is 60 miles. I am arbitrarily setting my location as the origin, and my home as the destination, and solving for the time.

As to why it is harder to integrate than differentiate ... it just is. It is easy to break the egg, and impossible to put it together again. Things don't have to be identical in effort in the reverse direction.

 

[FactChecker]

The equation for the derivative is the limit of a simple divided difference. And as the value of $\Delta x$ goes to the zero limit, it remains in a simple form. The equation for the integral is the limit of a sum of several terms, where the number of terms increase as the interval is divided more finely. That is much more difficult. The vast majority of integrals with a closed form equation are those where the integral and integrand are an antiderivative / derivative pair (i.e. the integrand is obtained from a relatively simple integral formula through differentiation).

 

[stevendaryl]

I don't know if this explains why integration is harder than differentiation, or is just another way of saying it, but...

In calculus, we tend to create complicated functions by composition of simpler functions. For example, from $e^x$ and $sin(x)$ we can get $e^{sin(x)}$. If you have two functions $f(x)$ and $g(x)$ and you know $f'$ and $g'$, then you can combine that knowledge to get $\frac{d}{dx} f(g(x))$: It's equal to $g'(x) f'(g(x))$.

In contrast, if you know the integral of $f$ and you know the integral of $g$, there is no simple way to combine those to get the integral of $f(g(x))$.

So in the case of differentiation, it's enough to know how to differentiate the basic functions, and that tells us how to differentiate much more complex functions. Integration doesn't work that way.

 

[FactChecker]

If you have two functions $f(x)$ and $g(x)$ and you know $f'$ and $g'$, then you can combine that knowledge to get $\frac{d}{dx} f(g(x))$: It's equal to $g'(x) f'(g(x))$.

In contrast, if you know the integral of $f$ and you know the integral of $g$, there is no simple way to combine those to get the integral of $f(g(x))$.

That's a very good point which may get to the heart of the matter.
That, together with the fact that integrals raise the power of $x^n$ rather than lowering it, give the derivative a great advantage when applied to two very basic operations.

 

[cosmik debris]

I didn't really understand these subtleties until a couple years after my first calculus sequence. Applications in physics helped, but what helped the most was when I finally got to a numerical analysis course and learned how to compute just about any derivative or integral numerically (and also how to integrate differential equations numerically. Somehow the computational approach (as opposed to the pencil and paper analytical approach) was the missing piece for my conceptual understanding.

Yes, we found that showing high school students how to write a program for integrating and differentiating gave them a much better understanding than the analytical approach.

Cheers

 

[haruspex]

or is just another way of saying it,

Yes, I feel your post neatly illustrates the sense in which integration is harder, but doesn't really constitute an explanation.
E.g. why are there not equivalents to the product rule and chain rule? (As Mark44 notes in post #9, integration by parts is equivalent to the product rule for differentiation, so is not an integration analogue of it.)
What would it look like?
Consider functions x=x(z) and y=y(z). Integrating up from z=0, ∫₀^cx.dz can be visualised as an area in the XZ plane between z=0 and z=c. Likewise, ∫₀^cy.dz in the YZ plane.
∫₀^cxy.dz, though, is a volume with those two shapes as faces and rectangular cross-section at each z.
Clearly we cannot deduce the volume merely from the two areas - it depends on the detailed interplay between x(z) and y(z) over the range of z. So it is not possible to write it in terms of x(c), y(c), ∫^cx and ∫^cy.

 

[Demystifier]

Is there a way to define the concept of indefinite integral without referring to the concept of a derivative? If no, or if it cannot be done in a simple way, then it could be the reason why analytical computation of indefinite integrals is harder than that of derivatives.

By the way, I remember that there is an advanced textbook on mathematical analysis that teaches integration before derivatives, but I cannot recall which textbook is that. Can someone refresh my memory?

 

[Demystifier]

Or perhaps the reason is the following. Suppose that function $f(x)$ is given for all $x$. From this, we want to determine the derivative $f'(x)$ and the anti-derivative $F(x)$. But instead of determining it at all points $x$, let us concentrate on one particular point $x_0$, say $x_0=7$. So now we only want to determine the two numbers $f'(x_0)$ and $F(x_0)$. The crucial difference is that the task of finding $f'(x_0)$ is well defined, while the task of finding $F(x_0)$ is meaningless. With fixed $f(x)$, the number $F(x_0)$ can be any number. Intuitively, this means that $f'(x)$ is a local property of a function $f(x)$, while $F(x)$ is a non-local property of a function $f(x)$. The $F$ only makes sense if it is defined in a finite neighborhood of a point $x_0$, while $f'$ can be defined at $x_0$ without knowing it in its neighborhood. Intuitively, determining something in a whole neighborhood should be more complicated than determining something at a single point.

 

[Demystifier]

By the way, I remember that there is an advanced textbook on mathematical analysis that teaches integration before derivatives, but I cannot recall which textbook is that. Can someone refresh my memory?

I found it!
https://www.amazon.com/dp/0387940014/?tag=pfamazon01-20

And for the record, I don't longer think that my argument in #54 is correct, but thanks for the likes!

 

[Svein]

The salient questions are:

1. If $f(x)$ is integrable, does $\frac{d}{dx}(\int f(x) dx)$ exist, and is it equal to $f(x)$ a. e.?
2. If $f(x)$ is differentiable on an open interval (a, b), will $\int_{a}^{x} (\frac{d}{dt} f(t))dt$ be equal to $f(x) - f(a)$?

Neither of these are trivial...

 

[OwlHoot]

Besides a lot of waffle about formalism and terminology, I'd suggest one answer to the OP's question is that differentiation is a "local" operation at a point whereas integration is a more "global" operation across a range of points. It isn't a foregone conclusion that the first must be simpler than the second, and I can think of examples where the opposite may be true. But that may be a suitable starting point for a type of answer that will satisfy the OP more than they seem to have been so far.

That aside, I think the best answer (already alluded to above) is integration's absence of a recursive procedure as effective as using the chain rule for differentiation, although integration by parts helps up to a point.

 

[e-pie]

An Analogy

Cutting a piece of paper into infinite strips is easy. Scissors make life easy. But joining them is hard. Glue sticks.

Same goes for integration and differentiation.

When you are differentiating a function, you are drawing tangents over the curve. Almost every curve has tangents but not all curve forms a closed area to integrate. Even if it forms it goes in the hyperbolic/complex domain. But differentiating real valued functions never gives a complex result. Because the tangents are all real line segments.