Teg Veece
- 8
- 0
I've been trying to evaluate an integral for the last few days now and it really has me stumped.
I was hoping that maybe someone here would be able to help me out.
So the function, cov(x,x'), is fairly basic. It's called a squared exponential covariance function and it evaluates the covariance between two points.
<br /> cov(x,x') = e^{-(\frac{r^2}{2l^2})}<br />
r is just the Euclidean distance between the points x and x'. l is the lengthscale constant for that dimension.
So for example the 1-D case, with an lengthscale of say 2, the covarance between a x = 5 and x' = 9 is:
<br /> cov(5,9) = e^{-\frac{1}{2}(\frac{(5-9)^2}{(3)^2})}= 0.4111<br />
In the 2-D case with an x lengthscale of 2 and a y lengthscale of 1 the covariance between x = (5,3) and x'=(9,6) is:
<br /> cov([5,3],[9,6]) = e^{-\frac{1}{2}(\frac{(5-9)^2}{3^2}+\frac{(3-6)^2}{1^2})}= 0.0046<br />So that's the function evaluated from a point to another point. However, I want to evaluate it from a point to a line segment.
I've solved this for the 1-D case but the 2-D case seems to be a bit trickier.
I've rewritten the covariance function so that it incorporates the equation of the line:
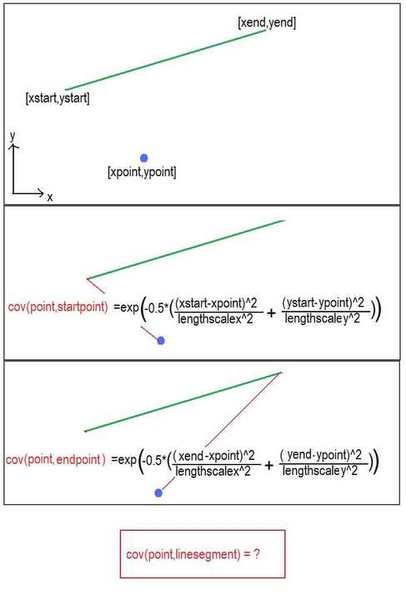
<br /> cov(([xstart,ystart],[xend,yend]),[xpoint,ypoint])=\int e^{-\frac{1}{2}(\frac{(x-xpoint)^2}{lengthscalex^2}+\frac{((mx+c)-ypoint)^2}{lengthscaley^2})}dx<br />
[xstart,ystart] are the starting coordinates of the line segment and [xend,yend] and the ending coordinates. [xpoint,ypoint] are the coordinates of the point. Everything in the equation is now a constant except for x. (m is the slope of the line segment and c is the y intercept of it)
So the limits of the integral would be xstart and xend.
I'm not sure how to integrate this however.
I have been able to get a solution by rotating the line segment and the point about the origin so that the line segment's slope is zero. Then it's very similar to the 1-D case. However is it possible to solve that integral without resorting to this.
Any help at all would be greatly appreciated. If you need me to clarify anything, just let me know.
I've summarised my problem in the pic below.
I was hoping that maybe someone here would be able to help me out.
So the function, cov(x,x'), is fairly basic. It's called a squared exponential covariance function and it evaluates the covariance between two points.
<br /> cov(x,x') = e^{-(\frac{r^2}{2l^2})}<br />
r is just the Euclidean distance between the points x and x'. l is the lengthscale constant for that dimension.
So for example the 1-D case, with an lengthscale of say 2, the covarance between a x = 5 and x' = 9 is:
<br /> cov(5,9) = e^{-\frac{1}{2}(\frac{(5-9)^2}{(3)^2})}= 0.4111<br />
In the 2-D case with an x lengthscale of 2 and a y lengthscale of 1 the covariance between x = (5,3) and x'=(9,6) is:
<br /> cov([5,3],[9,6]) = e^{-\frac{1}{2}(\frac{(5-9)^2}{3^2}+\frac{(3-6)^2}{1^2})}= 0.0046<br />So that's the function evaluated from a point to another point. However, I want to evaluate it from a point to a line segment.
I've solved this for the 1-D case but the 2-D case seems to be a bit trickier.
I've rewritten the covariance function so that it incorporates the equation of the line:
<br /> cov(([xstart,ystart],[xend,yend]),[xpoint,ypoint])=\int e^{-\frac{1}{2}(\frac{(x-xpoint)^2}{lengthscalex^2}+\frac{((mx+c)-ypoint)^2}{lengthscaley^2})}dx<br />
[xstart,ystart] are the starting coordinates of the line segment and [xend,yend] and the ending coordinates. [xpoint,ypoint] are the coordinates of the point. Everything in the equation is now a constant except for x. (m is the slope of the line segment and c is the y intercept of it)
So the limits of the integral would be xstart and xend.
I'm not sure how to integrate this however.
I have been able to get a solution by rotating the line segment and the point about the origin so that the line segment's slope is zero. Then it's very similar to the 1-D case. However is it possible to solve that integral without resorting to this.
Any help at all would be greatly appreciated. If you need me to clarify anything, just let me know.
I've summarised my problem in the pic below.
Last edited: