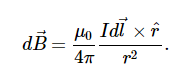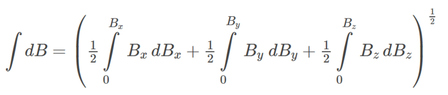Callumnc1 said:
Hi
@kuruman,
I looked into some vector calculus about integrating vector valued functions. I read that the
integral of a vector valued function (the magnetic field vector in this case)
is the integral of each component. however, now I would like to understand why there are no limits of integration for the RHS (
View attachment 318817).
I decided to add some and found that the limits below seem to work:
View attachment 318818
The textbook I'm using makes no mention why they did not include limits of integration and no mention of vector calculus. I guess the reason why they may not have included limits of integration is because they are summing all the small magnetic fields dB, but I would like to know the physical meaning of the limits of integration in this case.
Many thanks,
Callum
You are asking me for the physical meaning of the upper and lower limits to the integrals ##\int dB_x##, etc. I think I answered that in post #6. Let me first solve a simple problem where upper and lower have physical meaning.
A car is moving at constant acceleration ##a=4.0~##m/s
2. At ##t=3.0~##s its velocity is ##-2.0~## m/s. Find its velocity at ##t=5.0~##s.
You can solve this in your head. If the velocity of the car increases by ##4.0## m/s for every second that goes by, then from ##3.0## s to ##5.0## seconds, it will increase by ##8.0## m/s and will be ##-2+8=6~##m/s.
But the point is not to get the right answer but to illustrate the physical meaning of limits of integration. We start with the basic equation ##dv=a~dt## and integrate both sides. What limits of integration should we choose? Note that
(a) on the LHS we have dimensions of velocity and on the RHS we have dimensions of time.
(b) the lower and upper limits in the velocity must match the lower and upper limits in the time interval
(c) the upper limit that corresponds to the velocity at time ##t=5.0## s is unknown so we call it ##v.##
Integrating both sides, we write $$\begin{align} & \int_{-2.0~\text{m/s}}^v dv=\int_{3.0~\text{s}}^{5.0~\text{s}}4~(\text{m}/\text{s}^2)dt \nonumber \\
& v-(-2.0~\text{m/s})=4~(\text{m}/\text{s}^2)(5.0~\text{s}-3.0~\text{s}) \nonumber \\
& v+2.0~\text{m/s}=20.0~\text{m/s}-12.0~\text{m/s} \nonumber \\
& v=6.0~\text{m/s}. \nonumber
\end{align}$$Do you see the physical significance of the upper and lower limits and how they are arranged to match on the two sides? I chose non-zero lower limits to indicate to you that the lower limits is not zero unless there is a physical reason to be so.
The only physical meaning that the lower and upper limits of ##0## and ##B_x## that I can see is that zero is what you have for the sum before you start adding the x-components and ##B_x## is what you end up with when you're done adding. However, that is true for any sum regardless of what's on the RHS.
I have nothing more to say on this. If you still have questions, perhaps someone else will be able to answer them better than me.