SchruteBucks
- 13
- 0
Homework Statement
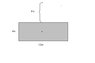
The picture attached shows an insulated board (12m x 4m) with uniform charge density σ. Integrate to find the electric field 8 cm above the center of the board.
Homework Equations
I found the equations \vec{E}=\int\frac{kdq}{r^{2}}\hat{r} and dq=σdy (both from google)
The Attempt at a Solution
We've never integrated to find anything in this class before so forgive my crude attempt...
I ended up with k\int^{10}_{6}\frac{σdy}{y^{2}}(-\hat{j})
I didn't put anything relating to the width of the board because I'm assuming its part of the density, with σ=Q/V=Q/48m2
Any help would be VERY much appreciated
Attachments
Last edited: