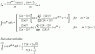Integrating with Gamma: cos(theta)^(2k+1)
- Thread starter Elliptic
- Start date
-
- Tags
- Gamma Integrating
Click For Summary
SUMMARY
The discussion focuses on solving the integral of cos(theta)^(2k+1) from 0 to π/2 and expressing it in terms of the gamma function. The standard method involves integration by parts, leading to a reducing formula that can be expressed as a ratio of factorials. Participants emphasize the importance of understanding the gamma function's relationship to factorials and suggest deriving the solution independently. The beta function is also mentioned as an alternative approach, providing a more elegant solution.
PREREQUISITES- Understanding of integration techniques, specifically integration by parts.
- Familiarity with the gamma function and its relationship to factorials.
- Knowledge of the beta function and its derivation.
- Basic trigonometric identities and properties of definite integrals.
- Study the derivation of the gamma function and its applications in calculus.
- Learn about the beta function and its relationship to the gamma function.
- Practice integration by parts with various trigonometric functions.
- Explore the cosine integral and its properties in mathematical analysis.
Students and educators in mathematics, particularly those studying calculus, integral equations, and special functions like the gamma and beta functions.
Similar threads
- · Replies 6 ·
- · Replies 19 ·
- · Replies 1 ·
- · Replies 5 ·
- · Replies 7 ·
- · Replies 2 ·
- · Replies 14 ·