TheGreatCabbage
- 4
- 0
New member has been reminded to fill out the Homework Help Template in future schoolwork threads
This isn't exactly homework or coursework, it is a past paper question that I cannot find a solution to (my university doesn't like releasing answers for some reason unknown to me).
The question is attached as an image (edit: the image displays while editing but not in the post, so I'll try to type it out):
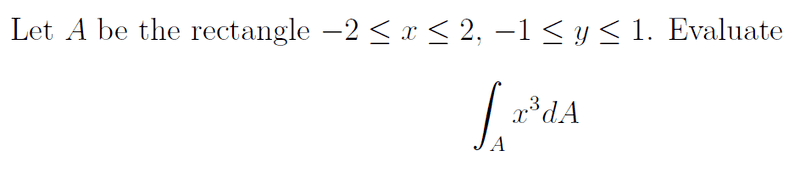
Question: Let A be the rectangle -2 ≤ x ≤ 2, -1 ≤ y ≤ 1. Evaluate ∫A x3 dA.
I attempted to solve this by parametising x and y in terms of a new variable t, such that x = 2t and y = t for -1 ≤ t ≤ 1. Then I used the fact that A = xy to obtain A = xy = 2t2 and dA = 4t dt. Substituting into the integral with limits -1 and 1 gave my a final answer of 64/5, but I lack confidence in my method and answer.
Should I use a double integral? Any help would be much appreciated.
The question is attached as an image (edit: the image displays while editing but not in the post, so I'll try to type it out):
Question: Let A be the rectangle -2 ≤ x ≤ 2, -1 ≤ y ≤ 1. Evaluate ∫A x3 dA.
I attempted to solve this by parametising x and y in terms of a new variable t, such that x = 2t and y = t for -1 ≤ t ≤ 1. Then I used the fact that A = xy to obtain A = xy = 2t2 and dA = 4t dt. Substituting into the integral with limits -1 and 1 gave my a final answer of 64/5, but I lack confidence in my method and answer.
Should I use a double integral? Any help would be much appreciated.