Sang Ho Lee
- 4
- 0
Hello, I'm currently taking calc 1 as an undergraduate student, and my professor just showed us a new? way of solving Integration By Parts.
This is the example he gave"
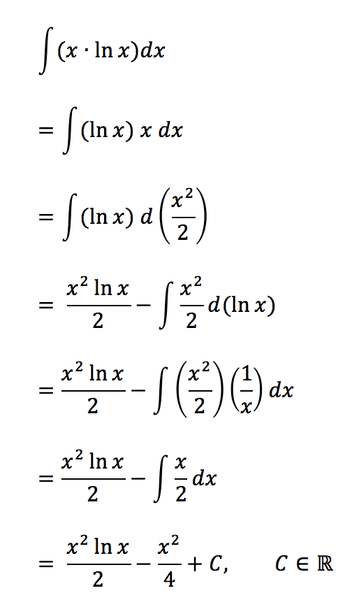
Is there a name for this technique that substitutes d(___) instead of dx?
Thank you,
This is the example he gave"
Is there a name for this technique that substitutes d(___) instead of dx?
Thank you,