- #1
bcjochim07
- 374
- 0
Integration Center of Mass Problem --Really frustrated
An 800 g steel plate has the shape of the isosceles triangle shown in the figure. What are the x and y coordinates of the center of mass?
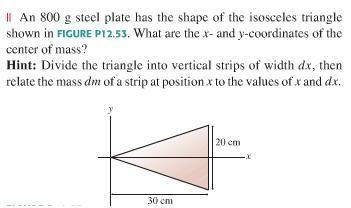
I am getting really frustrated with this one because I can't seem to relate dm to dx. I know that while dx is constant, dm is increasing because the height of the slices you cut the triangle into is increasing. Could someone please give me a push in the right direction? I am having trouble applying integration to center of mass problems.
Homework Statement
An 800 g steel plate has the shape of the isosceles triangle shown in the figure. What are the x and y coordinates of the center of mass?
Homework Equations
The Attempt at a Solution
I am getting really frustrated with this one because I can't seem to relate dm to dx. I know that while dx is constant, dm is increasing because the height of the slices you cut the triangle into is increasing. Could someone please give me a push in the right direction? I am having trouble applying integration to center of mass problems.