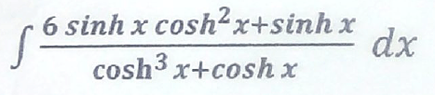SUMMARY
The discussion centers on solving the integral of the function involving hyperbolic sine and cosine, specifically the expression $$\int\dfrac{6\sinh(x)\cosh^2(x)+\sinh(x)}{\cosh^3(x)+\cosh(x)}\,dx$$. The integral is simplified using the identity for hyperbolic tangent, leading to the expression $$\int\tanh(x)\left(\dfrac{5\cosh^2(x)}{\cosh^2(x)+1}+1\right)\,dx$$. Participants are encouraged to continue solving the integral by breaking it down into manageable parts, including $$5\int\dfrac{\cosh(x)\sinh(x)}{\cosh^2(x)+1}\,dx$$ and $$\int\tanh(x)\,dx$$.
PREREQUISITES
- Understanding of hyperbolic functions, specifically sinh and cosh.
- Familiarity with integral calculus and techniques for solving integrals.
- Knowledge of hyperbolic identities and their applications in integration.
- Experience with mathematical notation and manipulation of integrals.
NEXT STEPS
- Study techniques for integrating hyperbolic functions, focusing on $$\int \tanh(x)\,dx$$.
- Learn about the properties and applications of hyperbolic identities in calculus.
- Explore advanced integration techniques, such as integration by parts and substitution methods.
- Practice solving complex integrals involving hyperbolic functions with varying degrees of difficulty.
USEFUL FOR
Students and professionals in mathematics, particularly those studying calculus and integral equations, as well as educators looking for examples of hyperbolic function integration.