Integrator Circuit Transfer Function (voltage divide)

[qwertyuiop23]

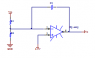
I have attached a picture of the circuit in which I am attempting to build a transfer function for, however, as you can see it is not a normal integrator. Normally it is evident which resistor is the resistor that is part of the series connection to the op amp.

When I do the KVL on the circuit to get the values I get the following function

<br /> <br /> v_{in} = C\frac{dv_{o}}{dt} + 2.5\times R_1 (\frac{1}{R1} + \frac{1}{R_2})

assuming that I voltage divide to 2.5V using values for R_1 = 5k\Omega R_2 = 910\Omega and the input is 16.3V.

<br /> v_{in} = C\frac{dv_{o}}{dt} + 16.23

From here I do not know how to get the transfer function. I am correct in assuming that the transfer function is no longer a linear line on the Bode plot due to that extra resistor that goes from the input to ground (thus reducing the current).

Or am I way off base with my assumptions.

Thank-you for your help
Lance

PS: I am an undergrad electrical engineer so the explanation does not have to be overly simplified.

 

[NascentOxygen]

You could solve the DE, then for sinusoids let v_in = A.sinѠt

Or you could start again, and let v_cap = i_C/(jѠc)
where i_C is the capacitor current

 

[qwertyuiop23]

That does make it more difficult to determine system dynamic parameters, ie rise time settling time and the such?

 

[NascentOxygen]

Your first post only mentioned Bode plot. If you are going to use Laplace, then let V_cap(s) = I_cap(s)/(s.C)

 

[qwertyuiop23]

Yes however, normally I use the Laplace form of the equation to make the transfer function to then recreate the Bode Plot.

The problem is that the Laplace transform is

<br /> <br /> sV_i = A s^2 V_o + B

As you can see the Constant B makes creating the transfer function very difficult!

 

[NascentOxygen]

What's that DC offset on op-amp's (+) input in aid ofhttp://physicsforums.bernhardtmediall.netdna-cdn.com/images/icons/icon5.gif You won't get anywhere while that's there, it will just send your op-amp output directly to the + rail! If that offset is to remain, then you'll need to exactly compensate for it by feeding DC into the (-) input, then superimpose your AC (for the Bode plot) on top of that DC. Capacitor coupling will achieve this.

Is this a circuit you invented as an exercise?