- #1
Graham87
- 63
- 16
- Homework Statement
- See pic
- Relevant Equations
- See pic
I can't figure out how they get i/sqrt(2) for normalisation of c1. Why is it a complex number? If I normalise c1 I just get 1/sqrt(2) because i disappears in the absolute value squared.
Thanks
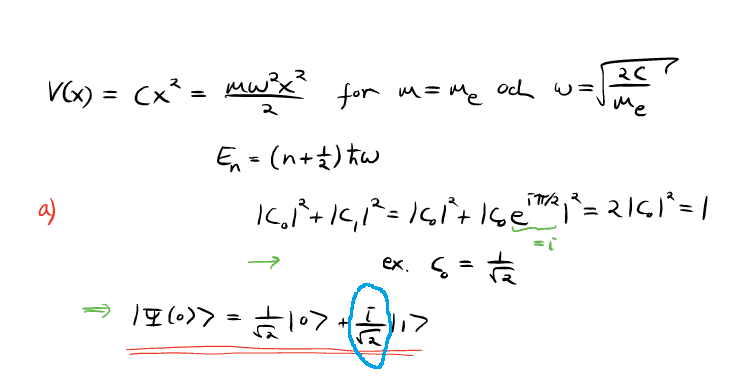
Thanks