Is a function better approximated by a line in some regions?

[Soren4]

I studied Taylor series but I would like to have an answer to a doubt that I have. Suppose I have $f(x)=e^{-x}$. Sometimes I've heard things like: "the exponential curve can be locally approximated by a line, furthermore in this particular region it is not very sharp so the approximation is even more good.."

Now I'm aware of the fact that any function (differentiable and so on) can be approximated by a line and further polynomial, but consider this graph of $f(x)$ and the regions $A$ and $B$.

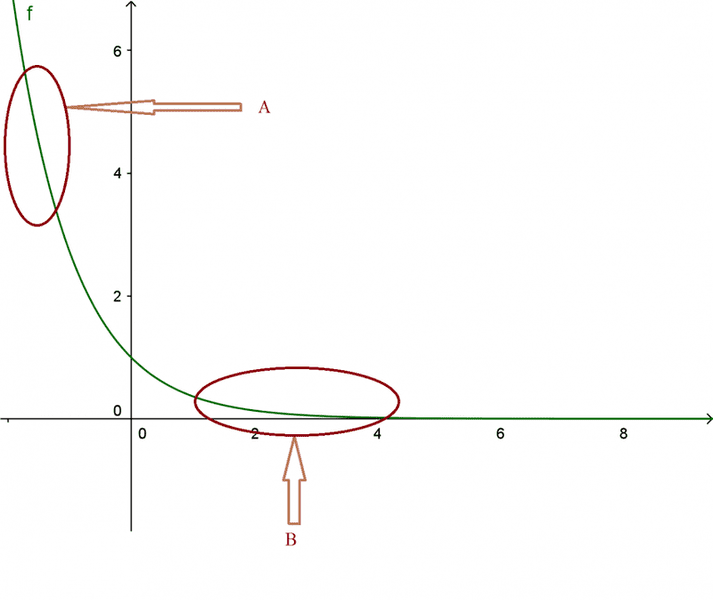
My question is : to what extent I can say "$f(x)$ is better approximated by a line in $B$ than in $A$"? And, if I could do this, why is that ? Is that because in region $B$ $f(x)$ is less sharp than in $A$, or is there other reason behind this?

 

[fresh_42]

If you consider a linear approximation, i.e. by the first derivative, then you have the Taylor series (expanded at a point $x_0$) written as
$f(x) = f(x_0) + (x-x_0) f'(x_0) + R(x,x_0)$ where the term $R(x,x_0)$ is the remainder, that makes the difference. So we have to consider this term. One way to write it, is $R(x,x_0) = \frac{1}{2} (x-x_0)^2 f''(\zeta)$ for a point $\zeta \in ]x,x_0[$.

Now you can choose a small interval around your points $x_0 = B$ and $x_0 = - \ln A$ and calculate the deviation $|R(x,x_0)|$ from linearity.

 

[fresh_42]

Another remark.
The formulation above isn't really good for numeric calculations, since it only states "there exists a certain $x < \zeta < x_0$ such that ..." and is of little use, if one actually needs to sharply calculate proper estimations. Here is where the work starts. If I remember correctly, there are several ways to get the hands on the remainders. Plural, because one can of course take more derivations into account than just one and get closer and closer towards $f$ and thus have according remainders $R$. (I would have searched the internet, if I knew the correct English term for $R$.)

However, the formulation above has a few advantages:
- it is easy to remember
- it can be used if one is interested in only a rough approximation
- it is sufficient for most physical applications (I think)

And finally it holds true for more than one term of the Taylor series, i.e.
$$f(x) = f(x_0) + (x-x_0)f'(x_0) + \frac{1}{2!}(x-x_0)^2f''(x_0) + \frac{1}{3!}(x-x_0)^3f^{(3)}(x_0) + \; \dots \; + \frac{1}{n!}(x-x_0)^nf^{(n)}(x_0) + R_n(x,x_0)$$
with now $R_n(x,x_0) = \frac{1}{(n+1)!}(x-x_0)^{n+1}f^{(n+1)}(\zeta)$

 

[Soren4]

Thanks a lot for your answers and your help!

I still do not really get if statements like the one in my question are somehow true or not... The remainder is bigger where $f''(\zeta)$ (the second derivative) is bigger, and there the approximation is worse. But here for istance, I understand that in both in regions $A$ and $B$ $f''$ is positive (by the way, why did you say to consider $B$ and $-lnA$? why the logarithm?) but I fail to understand where between $A$ and $B$ the second derivative is bigger, what could be the criteria to see where $f''$ is bigger in this case?

 

[fresh_42]

(by the way, why did you say to consider $B$ and $−lnA$? why the logarithm?)

Because you labeled $A$ on the $y-$axis and $B$ on the $x-$axis. For comparison you need some comparable ranges on the $x-$axis. The smaller you chose the interval $[x,x_0]$ the smaller is the deviation and it won't matter a lot whether $\zeta$ is closer at $x$ or at $x_0$ which we cannot know, since we only have the existence of such a $\zeta$ and not its position.