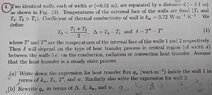SUMMARY
The discussion confirms that the heat transfer between two walls is independent of temperature assumptions when the positive direction for heat transfer fluxes is clearly defined. Specifically, defining the positive flow direction from external wall 2 to external wall 1 allows for valid equations regardless of the temperature values. This approach eliminates the need for specific temperature assumptions, streamlining the analysis of heat transfer scenarios.
PREREQUISITES
- Understanding of heat transfer principles
- Familiarity with thermal flux concepts
- Knowledge of wall temperature gradients
- Basic proficiency in thermodynamics equations
NEXT STEPS
- Research the implications of defining positive flow direction in heat transfer analysis
- Study the equations governing heat transfer between walls
- Explore case studies on heat transfer in multi-layer wall systems
- Learn about thermal conductivity and its role in heat transfer efficiency
USEFUL FOR
Engineers, physicists, and students studying thermodynamics or heat transfer, particularly those involved in building design and energy efficiency analysis.