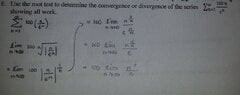Is My Root Test Solution Correct?

[Zoey93]

Hey,

I am working on this problem over the root test but I am not sure if I am doing it right. I will attach my work to this thread and I really want someone to look over my work and see if I am doing it right. By the way I didn't finish the problem because I was not sure where to go from my last step. Thank you!

View attachment 5149

 

[MarkFL]

I would agree that using the root test, we need only look at:

$$L=\lim_{n\to\infty}\sqrt[n]{\left|\frac{n}{e^n}\right|}=\frac{1}{e}\lim_{n\to\infty} n^{\frac{1}{n}}$$

I would next focus on:

$$L_1=\lim_{n\to\infty} n^{\frac{1}{n}}$$

If we take the natural log of both sides, we obtain:

$$\ln\left(L_1\right)=\lim_{n\to\infty} \frac{\ln(n)}{n}$$

From this, can you now determine $L_1$, and hence $L$?

 

[suluclac]

Converges absolutely