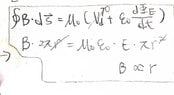Is the Induced Electric Field Proportional to Radius in a Cylindrical Region?

[hidemi]

Homework Statement

A cylindrical region of radius R contains a uniform magnetic field, parallel to its axis, with magnitude that is changing linearly with time. If r is the radial distance from the cylinder axis, the magnitude of the induced electric field inside the cylindrical region is proportional to

A) R
B) r
C) r²
D) 1/r
E) 1/ r²

The answer is B.

Relevant Equations

(See better interpretation in the "Attempt at a Solution" section)

I used the equation below and the attachment to rationalize.
https://www.physicsforums.com/attachments/282163

 

[Delta2]

You used Ampere-Maxwell law while you should use Faraday-Maxwell Law. The problem statement asks for the magnitude of the electric field. There is no time-varying electric flux in this problem setup (so $\frac{d\Phi_E}{dt}=0$ but there is time-varying magnetic flux (linearly time varying)).

 

[hidemi]

E * 2πr = - B * π r²
E = B * r /2
Therefore, E is proportional to r. Is this correct?

 

[Delta2]

E * 2πr = - B * π r²
E = B * r /2
Therefore, E is proportional to r. Is this correct?

Yes the above is correct.

 

[rude man]

E * 2πr = - B * π r²
E = B * r /2
Therefore, E is proportional to r. Is this correct?

Change B to dB/dt (= constant).