Discussion Overview
The discussion revolves around the question of whether the sum of torques is zero in a system where two equal forces act at equal distances from a pivot point, particularly when the forces are applied in a non-linear medium. Participants explore the implications of equal forces and moment arms on torque and motion, considering scenarios of both equal and unequal forces.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
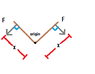
- One participant questions if the sum of torques is zero when equal forces are applied at equal moment arms in a non-linear medium.
- Another participant notes that without a visual aid, the context is unclear but suggests that equal and opposite forces acting along a common line would not produce torque.
- A later reply asserts that for equal forces at right angles to equal moment arms, the sum of torques would indeed be zero.
- Some participants mention that if forces are unequal, there would be a resultant torque, but if they are made equal, the system could achieve uniform circular motion.
- One participant emphasizes that the forces could act on the same arm with zero angle between them, yet still result in zero torque.
- Concerns are raised about the need for a reaction force at the pivot to maintain circular motion without linear acceleration.
Areas of Agreement / Disagreement
Participants express differing views on the conditions under which the sum of torques is zero, with some agreeing that equal forces lead to zero torque while others highlight the complexity introduced by the medium and the need for additional forces to maintain equilibrium. The discussion remains unresolved regarding the implications of the forces' arrangement and the medium's influence.
Contextual Notes
Participants do not reach a consensus on the impact of the angle between moment arms or the specific configuration of forces, indicating that assumptions about the system's behavior may vary based on these factors.