Python Is there a Python function that finds an unknown inside an integral?

[Arman777]

I have a integral with unknown h. My integral looks like this

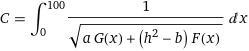
where C, a, b are constants F(x) and G(x) are two functions. So the only unknows in the integral is h. How can I solve it ? I guess I need to use scipy but I don't know how to implement or use which functions.

Thanks

 

[jedishrfu]

Perhaps something like this:

https://stackoverflow.com/questions...unknown-inside-the-upper-limit-of-an-integral

 

[Timo]

One approach would be to define f(h) = the_integral(h) - C, and then use some scipy root solver to find h such that f(h) = 0.

 

[pasmith]

Using Newton's method.

Integration is done using scipy.integrate.quad_vec in order to evaluate the function and its derivative at the same time. (We can't do this if we use scipy.optimize.fsolve; we would have to pass the function and its derivative as separate arguments.)

from scipy.integrate import quad
import numpy as np

# An initial guess for h. Change this to something more suitable.
h0 = 1.0

# Loop terminates if absolute difference between successive approximations 
# is less than this.
tol = 1E-6

h_new = h0
h_old = hnew + 2*tol
while abs(h_old - h_new) >= tol:
   h_old = h_new

   # Compute integral at h_old as well as its derivative with respect to h
   res = quad_vec(
      lambda x : np.array([
         1/np.sqrt(a*G(x) + (h_old**2 - b)*F(x)), 
         -3*np.sqrt(a*G(x) + (h_old**2 - b)*F(x))**(-3) * h_old * F(x)
      ]),
      0, 100
   ) 
   
   # The actual value is res[0]. Other elements may contain error indications
   # which you should check before continuing. See the documentation for details.

   # New guess
   h_new = h_old - (res[0][0] - C)/res[0][1]

# h_new now contains the estimated value of h.