bcjochim07
- 366
- 0
Is this correct? -- Gas Law Question
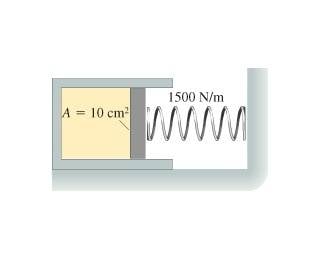
The cylinder in the figure has a moveable piston attached to a spring. The cylinder's cross sectional area is 10 cm^2 and it contains .005 mol of gas. The spring constant is 1500 N/m. At 16 degrees Celsius, the spring is neither stretched nor compressed. How far is the spring compressed when the gas temperature is raised to 160 degrees Celsius?
P1/T1 = P2/T2
16 degrees C = 289 K 160 degrees C = 433 K
10cm^2 * (1m/100cm)^2 = .001 m^2
Since the spring is not exerting any force on the piston initially, the pressure inside the cylinder is equal to the air pressure (1 atm = 101300 Pa)
(101300 Pa)/(289K) = P2/(433 K)
P2=151775 Pa and P2= (1500N/m)x/(.001 m^2) + (101300 Pa)
x=.034 m = 3.4 cm
Homework Statement
The cylinder in the figure has a moveable piston attached to a spring. The cylinder's cross sectional area is 10 cm^2 and it contains .005 mol of gas. The spring constant is 1500 N/m. At 16 degrees Celsius, the spring is neither stretched nor compressed. How far is the spring compressed when the gas temperature is raised to 160 degrees Celsius?
Homework Equations
The Attempt at a Solution
P1/T1 = P2/T2
16 degrees C = 289 K 160 degrees C = 433 K
10cm^2 * (1m/100cm)^2 = .001 m^2
Since the spring is not exerting any force on the piston initially, the pressure inside the cylinder is equal to the air pressure (1 atm = 101300 Pa)
(101300 Pa)/(289K) = P2/(433 K)
P2=151775 Pa and P2= (1500N/m)x/(.001 m^2) + (101300 Pa)
x=.034 m = 3.4 cm