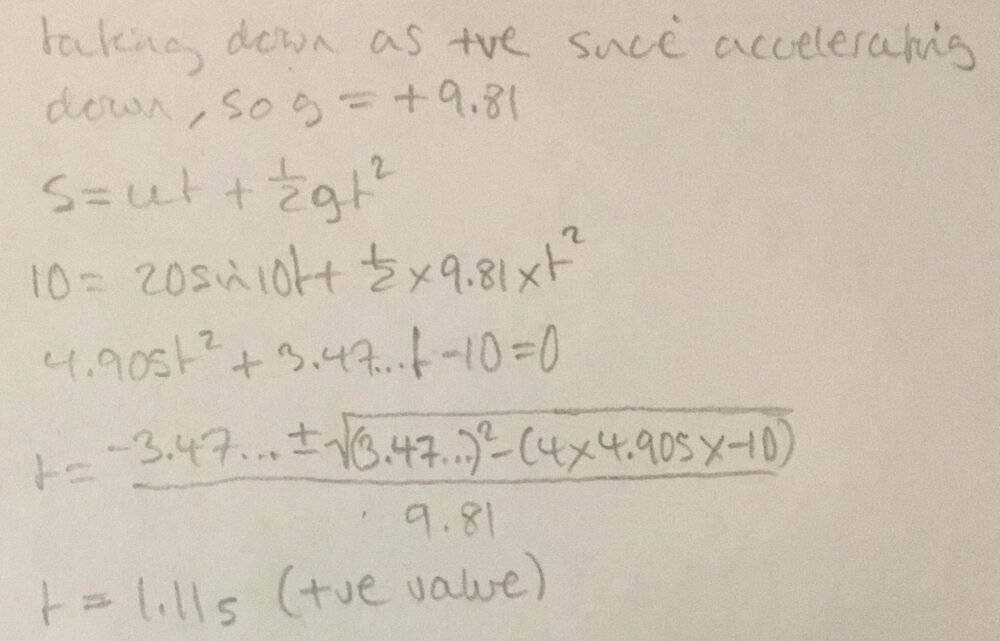so_gr_lo
- 69
- 10
- Homework Statement
- Find time of flight of particle projected down at 10° to horizontal at initial speed 20 ms^-1 at height 10m.
- Relevant Equations
- s = ut -1/2at^2
These questions normally have initial velocity = 0, so that one of the t terms cancels. In this case u = 20ms^-1 so I end up with a quadratic. Which is fine if I plug it into the quadratic formula as one result is -ve so can be ignored, while the other gives t as +ve. just wondering if this is the correct way of calculating the time of flight. Attempt at question below