Hill
- 812
- 627
- Homework Statement
- Draw an arbitrary triangle, and on each side draw an equilateral triangle lying outside the given triangle. What do you suspect is special about the new triangle formed by joining the centroids (cf. Ex. 19) of the equilateral triangles?
Use complex algebra to prove that you are right.
What happens if the equilateral triangles are instead drawn on the inside of the given triangle?
- Relevant Equations
- from the "Ex.19", centroid g of a triangle abc is g=1/3(a+b+c)
Here is my sketch:
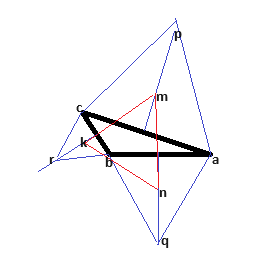
The triangle ##abc## is arbitrary, the triangles ##acp##, ##abq##, and ##bcr## are equilateral with centroids ##m##, ##n##, and ##k##. I suspect that the triangle ##mnk## is equilateral. Here is my proof.
By the equation for centroids,
##3m=a+c+p##
##3n=a+q+b##
##3k=b+c+r##
Let's show that angle between ##\vec {mk}## and ##\vec {mn}## is ##\pi /3##.
##3 \vec {mk} = 3(k-m)=(b+c+r)-(a+c+p)=(b-a)+(r-p)=\vec {ab} + \vec {pr}=\vec {ab}+\vec{pc}+\vec{cr}##
##3 \vec {mn} = 3(n-m)=(a+q+b)-(a+c+p)=(b-c)+(q-p)=\vec {cb} + \vec {pq}=\vec {cb}+\vec{pa}+\vec{aq}##
Let ##R## be rotation by ##\pi /3##, i.e., multiplication by ##e^{i \pi /3}##. Then
##R(3 \vec {mk})=R(\vec {ab})+R(\vec{pc})+R(\vec{cr})=\vec{aq}+\vec{pa}+\vec {cb}=3 \vec {mn}##
Done.
If the equilateral triangles are instead drawn on the inside of the given triangle, then R should rotate in opposite sense, i.e., should be replaced by ##e^{-i \pi /3}##.
My questions:
1. Does this proof "use complex algebra"?
2. Is there a more direct proof?
3. Is there anything else "special about the new triangle"?
The triangle ##abc## is arbitrary, the triangles ##acp##, ##abq##, and ##bcr## are equilateral with centroids ##m##, ##n##, and ##k##. I suspect that the triangle ##mnk## is equilateral. Here is my proof.
By the equation for centroids,
##3m=a+c+p##
##3n=a+q+b##
##3k=b+c+r##
Let's show that angle between ##\vec {mk}## and ##\vec {mn}## is ##\pi /3##.
##3 \vec {mk} = 3(k-m)=(b+c+r)-(a+c+p)=(b-a)+(r-p)=\vec {ab} + \vec {pr}=\vec {ab}+\vec{pc}+\vec{cr}##
##3 \vec {mn} = 3(n-m)=(a+q+b)-(a+c+p)=(b-c)+(q-p)=\vec {cb} + \vec {pq}=\vec {cb}+\vec{pa}+\vec{aq}##
Let ##R## be rotation by ##\pi /3##, i.e., multiplication by ##e^{i \pi /3}##. Then
##R(3 \vec {mk})=R(\vec {ab})+R(\vec{pc})+R(\vec{cr})=\vec{aq}+\vec{pa}+\vec {cb}=3 \vec {mn}##
Done.
If the equilateral triangles are instead drawn on the inside of the given triangle, then R should rotate in opposite sense, i.e., should be replaced by ##e^{-i \pi /3}##.
My questions:
1. Does this proof "use complex algebra"?
2. Is there a more direct proof?
3. Is there anything else "special about the new triangle"?