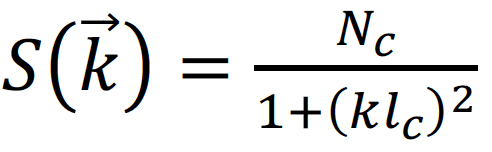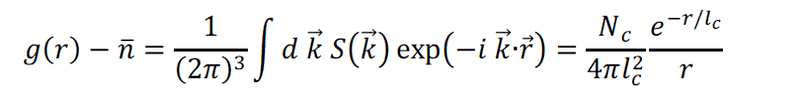SUMMARY
The discussion centers on the application of the Ornstein-Zernike equation to isotropic materials. The user is attempting to derive the pair correlation function but encounters difficulties. They mention a specific integral evaluation involving the residue theorem, which yields the desired results. The integral in question is $$\frac{N_c}{4\pi^3r}\int_{-\infty}^{\infty}dk\frac{e^{-ikr}}{1+k^2l_c^2}$$, indicating a complex analysis approach to solving the problem.
PREREQUISITES
- Understanding of the Ornstein-Zernike equation
- Familiarity with isotropic materials in statistical mechanics
- Knowledge of complex analysis, specifically the residue theorem
- Proficiency in evaluating integrals in the context of physics
NEXT STEPS
- Study the derivation of the Ornstein-Zernike equation in detail
- Learn about pair correlation functions in statistical mechanics
- Explore complex analysis techniques, particularly the residue theorem
- Investigate applications of isotropic materials in physical systems
USEFUL FOR
Researchers in statistical mechanics, physicists working with isotropic materials, and students studying complex analysis in the context of physical applications.