Jacobson Radical and Direct Sums - Bland, Proposition 6.1.4

[Math Amateur]

I am reading Paul E. Bland's book, "Rings and Their Modules".

I am focused on Section 6.1 The Jacobson Radical ... ...

I need help with the proof of Proposition 6.1.4 ...Proposition 6.1.4 and its proof read as follows:

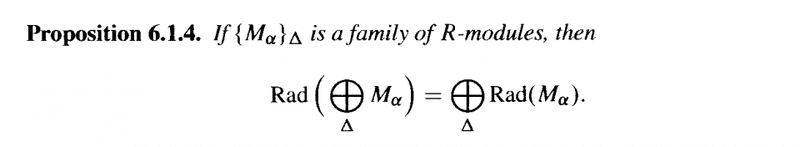
In the above proof from Bland we read:"... ... If $i_1 \ : \ M_1 \longrightarrow M_1 \oplus M_2$ and $i_2 \ : \ M_2 \longrightarrow M_1 \oplus M_2$ are the canonical injections, then (a) of Exercise 3 shows that

$i_k \ : \ \text{ Rad}(M_k) \longrightarrow \text{ Rad}(M_1 \oplus M_2)$ ... ...

... ... ... "
My question/problem/issue is that I cannot understand the meaning of the statement that (a) of Exercise 3 shows that

$i_k \ : \ \text{ Rad}(M_k) \longrightarrow \text{ Rad}(M_1 \oplus M_2)$ ... ...How, exactly, do the canonical injections $i_k$ apply to $\text{ Rad}(M_k)$ and $\text{ Rad}(M_1 \oplus M_2)$ ... ...

Is it trivially simple in that $\text{ Rad}(M_k)$ is a set of elements of $M_k$ and so the canonical injection operates as usual? But then... why do we need Exercise 3?

Can someone explain in simple terms ... ... exactly what is going on ...

Peter

=============================================================================
NOTE ... ... The above post refers to Exercise 3 of Bland, Section 6.1 so I am providing the text of that example ... as follows:

 

[fresh_42]

In the above proof from Bland we read:
"... ... If $i_1 \ : \ M_1 \longrightarrow M_1 \oplus M_2$ and $i_2 \ : \ M_2 \longrightarrow M_1 \oplus M_2$ are the canonical injections, then (a) of Exercise 3 shows that

$i_k \ : \ \text{ Rad}(M_k) \longrightarrow \text{ Rad}(M_1 \oplus M_2)$ ... ..."

My question/problem/issue is that I cannot understand the meaning of the statement that (a) of Exercise 3 shows that

$i_k \ : \ \text{ Rad}(M_k) \longrightarrow \text{ Rad}(M_1 \oplus M_2)$ ... ...

How, exactly, do the canonical injections $i_k$ apply to $\text{ Rad}(M_k)$ and $\text{ Rad}(M_1 \oplus M_2)$ ... ...

Hi Peter,

it is a direct application of the statement in exercise 3.
For any $R-$homomorphism $f\, : \,M \rightarrow N$ of $R-$modules we have $f(rad(M)) \subseteq rad(N)$.

Now chose $M:=M_1\, , \,N:=M_1\oplus M_2\, , \,f := \iota_1 \, , \,M_1 \subseteq M_1\oplus M_2$ and ex.3 says $\iota_1(rad(M_1)) = rad(M_1) \subseteq rad(M_1\oplus M_2)$
The same goes of course for $M_2$ and $\iota_2(rad(M_2)) = rad(M_2) \subseteq rad(M_1\oplus M_2)$
Therefore $rad(M_1) \oplus rad (M_2) \subseteq rad(M_1\oplus M_2)$.

For the proof of exercise 3 with $f$ an $R-$homomorphism $f\, : \,M \rightarrow N$ of $R-$modules we consider an arbitrary maximal submodule $N' \subsetneq N$ and the projection $\pi\, : \,N \twoheadrightarrow N/N'$ onto the simple module $N/N'$ and the map $\varphi := \pi \circ f\, : \, M \rightarrow N/N'\,.$ Then we must show that $M':=ker \varphi$ is a maximal submodule of $M$ and thus contains $rad(M)\,.$ If you haven't done it already you should try to prove it and fill the gaps in my outline.

 

[mathwonk]

just a guess, in the next to last line, did you mean: "kerphi is either a maximal (proper) submodule of M or the whole module M" ?by the way, just curious, if a module M has no proper maximal submodules, is the jacobson radical equal to M?

 

[fresh_42]

just a guess, in the next to last line, did you mean: "kerphi is either a maximal (proper) submodule of M or the whole module M" ?

I did not mention this special case, yes.
$rad (M) \subseteq M = ker \varphi \Rightarrow \varphi =0 \Rightarrow \varphi(rad(M)) = \{0\} \Rightarrow f(rad(M)) \subseteq ker(\pi) = N'\,.$
and the rest of the argument is the same as in the case $M'\subsetneq M\,.$

by the way, just curious, if a module M has no proper maximal submodules, is the jacobson radical equal to M?

Yes, by convention. We've had an interesting discussion of this case here:
https://www.physicsforums.com/threads/jacobson-radical-and-rad-m-bland-corollary-6-1-3.898836/