Hello John,
If you were trying to compute the volume of the resulting tank, then either the shell or disk method would be appropriate, but we are computing the work done to empty the tank, so we want to decompose the volume into disks, since each disk will have all parts at the same gravitational potential energy.
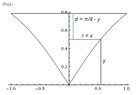
Let's first take a look at a cross-section of the tank through the axis of symmetry:
View attachment 1153
The radius $r$ of an arbitrary slice I have drawn in red and the distance $d$ through which it must be lifted is drawn in green. We know the amount of work required to lift this slice is the product of the applied force and the distance over which this force is applied, hence:
$$dW=Fd$$
Now, the applied force is simply the weight of the slice:
$$F=mg$$
and the mass of the slice is the product of its mass density $\rho$ and it volume $V$:
$$m=\rho V$$
and of course the volume of the slice is:
$$V=\pi r^2\,dy$$
where the radius of the slice is:
$$r=x=\tan(y)$$
Now, putting this together, we find:
$$dW=Fd=(mg)\left(\frac{\pi}{4}-y \right)=(g\rho V)\left(\frac{\pi}{4}-y \right)=g\rho\left(\pi r^2\,dy \right)\left(\frac{\pi}{4}-y \right)=\pi g\rho\tan^2(y)\left(\frac{\pi}{4}-y \right)\,dy$$
Summing up all the elements of work, we obtain:
$$W=\pi g\rho\int_0^{\frac{\pi}{4}}\tan^2(y)\left( \frac{\pi}{4}-y \right)\,dy$$
Applying Simpson's Rule with $n=6$ on the integral, where:
$$f(y)=\tan^2(y)\left( \frac{\pi}{4}-y \right)$$
and:
$$y_k=\frac{\frac{\pi}{4}-0}{6}k=\frac{\pi}{24}k$$ with $$k\in\{0,1,2,3,4,5,6\}$$
we find:
$$S_6=\frac{\frac{\pi}{4}-0}{3(6)}\left[f\left(y_0 \right)+4f\left(y_1 \right)+2f\left(y_2 \right)+4f\left(y_3 \right)+2f\left(y_4 \right)+4f\left(y_5 \right)+f\left(y_6 \right) \right]$$
$$S_6=\frac{\pi}{72}\left[f\left(y_0 \right)+4f\left(y_1 \right)+2f\left(y_2 \right)+4f\left(y_3 \right)+2f\left(y_4 \right)+4f\left(y_5 \right)+f\left(y_6 \right) \right]$$
$$f\left(y_0 \right)=f\left(\frac{\pi}{24}\cdot0 \right)=f(0)=\tan^2(0)\left( \frac{\pi}{4}-0 \right)=0$$
$$4f\left(y_1 \right)=4f\left(\frac{\pi}{24}\cdot1 \right)=4f\left(\frac{\pi}{24} \right)=4\tan^2\left(\frac{\pi}{24} \right)\left( \frac{\pi}{4}-\frac{\pi}{24} \right)\approx0.045376065047798$$
$$2f\left(y_2 \right)=2f\left(\frac{\pi}{24}\cdot2 \right)=2f\left(\frac{\pi}{12} \right)=2\tan^2\left(\frac{\pi}{12} \right)\left( \frac{\pi}{4}-\frac{\pi}{12} \right)\approx0.075185401439313$$
$$4f\left(y_3 \right)=4f\left(\frac{\pi}{24}\cdot3 \right)=4f\left(\frac{\pi}{8} \right)=4\tan^2\left(\frac{\pi}{8} \right)\left( \frac{\pi}{4}-\frac{\pi}{8} \right)\approx0.269506042226324$$
$$2f\left(y_4 \right)=2f\left(\frac{\pi}{24}\cdot4 \right)=2f\left(\frac{\pi}{6} \right)=2\tan^2\left(\frac{\pi}{6} \right)\left( \frac{\pi}{4}-\frac{\pi}{6} \right)\approx0.174532925199433$$
$$4f\left(y_5 \right)=2f\left(\frac{\pi}{24}\cdot5 \right)=4f\left(\frac{5\pi}{24} \right)=4\tan^2\left(\frac{5\pi}{24} \right)\left( \frac{\pi}{4}-\frac{5\pi}{24} \right)\approx0.308290092997036$$
$$f\left(y_6 \right)=f\left(\frac{\pi}{24}\cdot6 \right)=f\left(\frac{\pi}{4} \right)=\tan^2\left(\frac{\pi}{4} \right)\left( \frac{\pi}{4}-\frac{\pi}{4} \right)=0$$
Adding these together, we find:
$$S_6\approx0.0380870342601150$$
For comparison, a numeric integration function returns:
$$0.038148452745930$$
Now, using the approximation we obtained, we may state:
$$W\approx\pi g\rho\cdot0.0380870342601150$$
Using the given data:
$$g=9.8\frac{\text{m}}{\text{s}^2},\,\rho=1000\frac{\text{kg}}{\text{m}^3}$$
and observing the integral has units of $\text{m}^4$, we have:
$$W\approx\pi\left(9.8\frac{\text{m}}{\text{s}^2} \right)\left(1000\frac{\text{kg}}{\text{m}^3} \right)\cdot0.0380870342601150\text{ m}^4\approx1172.60868088\text{ J}$$
For comparison, the exact answer is:
$$W=\frac{1225\pi}{4}\left(16\ln(2)-\pi^2 \right)\text{ J}\approx1174.5\text{ J}$$