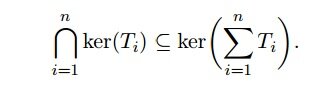Kernel on linear transformation proof
- Context: MHB
- Thread starter Cristian1
- Start date
Click For Summary
SUMMARY
This discussion focuses on proving that if a vector \( v \) belongs to the intersection of the kernels of multiple linear transformations \( T_1, T_2, \ldots, T_n \), then it also belongs to the kernel of their sum \( \sum_{i=1}^{n} T_i \). The proof is established by demonstrating that \( T_i(v) = 0 \) for each transformation, leading to \( \sum_{i=1}^{n} T_i(v) = 0 \). An example using \( \mathbb{R}^3 \) illustrates the concept, showing that the intersection of the kernels corresponds to specific geometric planes.
PREREQUISITES- Understanding of vector spaces and linear transformations
- Familiarity with kernel and image concepts in linear algebra
- Basic knowledge of set theory and intersections
- Ability to perform vector operations in \( \mathbb{R}^n \)
- Study the properties of linear transformations in depth
- Learn about the Rank-Nullity Theorem in linear algebra
- Explore examples of kernel intersections in higher dimensions
- Investigate applications of linear transformations in computer graphics
Students and professionals in mathematics, particularly those studying linear algebra, as well as educators seeking to clarify concepts related to linear transformations and their properties.
Similar threads
- · Replies 1 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 3 ·
- · Replies 9 ·
- · Replies 23 ·
- · Replies 7 ·
- · Replies 9 ·
- · Replies 4 ·
- · Replies 3 ·