Kirchhoff's law: Find the current I3 through the Amp meter

[skibidi]

Homework Statement

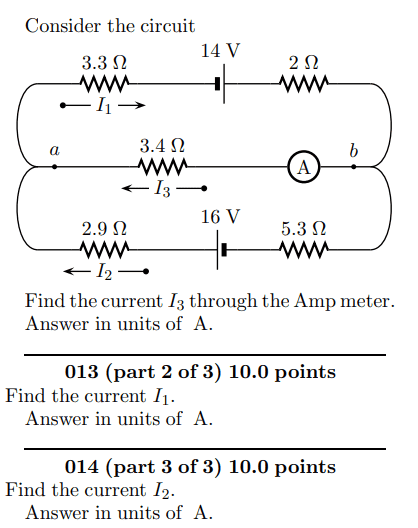
Find the current I3,I2, and I1 through the Amp meter.
Answer in units of A.

Relevant Equations

I used the Junction Rule - I3= I1+I2

I separated the circuit into parts- upper and lower

For the upper loop I wrote: -14-2I1-3.4I3-I2 = 0
For the lower loop I wrote 16-2.9I2+3.4I3-5.4I2 = 0

I solved for I1 and I2 separately and plugged it into the junction rule and solved for I3.

I may have got it wrong because of the incorporation of the extra resistor in the upper loop and lower loop and solved incorrectly.

 

[skibidi]

Correction for the problem after i found I3 correctly now.

The correct equation is now -14+3.3(I1)+3.4(I3)+2(I1)= 0 for the upper loop and
-16+5.3(I2)-3.4(I3)+2.9(I2) = 0 for the bottom loop. Once you separate variables, I2 = stuff and I1 = stuff, you can use the junction rule I1 = I2+I3 and rearrange to get I1-I2=I3. Plug it in and you should get I3 = 0.336A

 

[skibidi]

Use I3 to get I2 and I1 since you have separate equations for them already -

I1 = -3.4(I3)+14/5.3 and I2 = 3.4(I3) +16/ 8.2

I1 = 2.43 A , I2 = 2.09 A

 

[skibidi]

If anyone else sees this, can you verify that my explanation is correct since I was able to get the correct answers on my own.

 

[Gavran]

$\text { The explanation is correct, but the result can be more accurate. }$

$3,3 \Omega \cdot 2,43 A + ( - 14 ) V + 2 \Omega \cdot 2,43 A + 3,4 \Omega \cdot 0,336 A =$
$= 8,0058 V – 14 V + 4,852 V + 1,1424 V =$
$= 0,0214 V \neq 0 V$
$\text { It is hard to say that Kirchhoff Voltage Law is satisfied for the upper loop because it is hard to say that } 0,0214 V \text { is equal to } 0 V \text { . }$
$\text { The more accurate result can be got rounding the value of } I _ 1 \text { to } 2,426 A \text { instead of } 2,43 A \text { . }$
$\text { Values of } I _ 2 \text { , which is } 2,090 A \text { , and } I _ 3 \text { , which is } 0,336 A \text { , can remain the same. }$