Undergrad Kronecker delta by using creation/annihilation operators

[Faust90]

Hey all,

i've found the following expression:

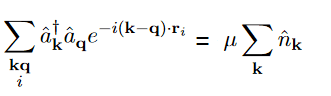
How do they get that? They somehow used the kronecker delta Sum_k exp(i k (m-n))=delta_mn. But in the expression above, they're summing over i and not over r_i??

Best

 

[Faust90]

Do you need more background or is the question not precise enough? :-)

 

[Mr-R]

Hi Faust90

The index $i$ under the sum refers to the subscript $i$ under the $r$. The other i is the imaginary number. The Kronecker delta gets rid of the exponential and thus the sum on $i$ anyway. Try this website and see if it clears any confusion you are having. http://www.physicspages.com/2014/11/09/discrete-fourier-transforms/

 

[Faust90]

Hi Mr-R,

thanks for your answer. Yes, but my problem is that the sum is not running over r_i but over i.
Let's assume the r_i are an set of positions, for example always the same position, i.e. r_i={1,1,1,1,1,1,...}. Then in the end, that's just a product
prod_n=0^\infity e^{i(k-q)}