Lagrange Multipliers: A theoretical question and an example

[diewolke]

Hello physicsforums community.
I have recently learned about Lagrange multipliers and have been given three problems to solve. Could you guys please go over my work and see if I have the gist of it? One question, a theoretical one, I have no idea how to begin. Any advice regarding this would be welcomed.

Thanks

PS: Please excuse any formatting errors; this is my first post on this forum.

--------------

Question 1a

f:R^2-->R^2, (x,y)-->x^2-y^2, and let S be the circle of radius 1 around the origin.
In two dimensions, the condition that
$$\nabla$$f(x,y,z)=$$\lambda$$$$\nabla$$g(x,y,z) at $$x_{o}$$, that is, $$\nabla$$f(x,y,z) and $$\nabla$$g(x,y,z) are parallel at $$x_{o}$$[/tex] is the same as the level curves being tangent at x$$_{.}$$. Give the reason why you may conclude that the level curves are tangent at $$x_{o}$$.

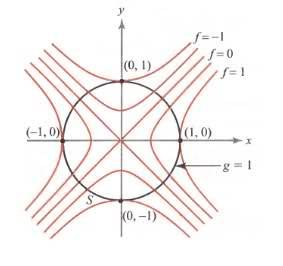
2. f:R^2-->R^2, (x,y)-->x^2-y^2 and
g:R^2-->R^1, (x,y)--> x^2+y^2 (obtained from the statement about S)


3. I simply do not have a clue how to go about this. I know that the gradient of a function is given by the coordinates which are the function's partial derivatives. I also know that the gradient points to the direction of highest increase for a function at a particular point. Regarding level sets, I know that level sets are given by all (x,..x$$_{n}$$) such that f(x,..,x$$_{n}$$)=c, where c is a constant. I am not sure how to utilize this information to produce an answer. Any advice?


---------------

Question 1b
1. Using the Lagrange multiplier method, maximize the function f(x,y,z)=x+z subject to the constraint x^2+y^2+z^2=51

2. $$\nabla$$f(x,y,z)=$$\lambda$$$$\nabla$$g(x,y,z)

3.
Having computed the gradients for g and f, listed the partials separately, and using the above equation, I obtained the following system of equations:
1=2x$$\lambda$$
0=2y$$\lambda$$
1=2z$$\lambda$$

Solving for x, y, and z, I obtained
x=1/(2lambda)
y=0 and
z=x=1/(2lambda)

and here is the constraint once more: x^2+y^2+z^2=51
substituting the values of x, y, and z into the above expression,
I get $$\lambda$$=+ or - $$\frac{1}{\sqrt{102}}$$

using this value to solve for x, y, and z, I get that
x=+ or -$$\frac{\sqrt{102}}{2}$$
y=0 and
z=+ or -$$\frac{\sqrt{102}}{2}$$

plugging in these values into f(x,y,z)=x+z,
I find that the max must be $$\sqrt{102}$$. Is this correct?
----------

I will post the third question shortly.

Thank you again

 

[diewolke]

Question 2
1. Consider the function f(x,y)=5/x+1/y subject to the constraint
x+y=1, x>0, and y>0. Does this function with a constraint have a minimum or maximum? If so, what are these values?

2. $$\nabla$$f(x,y)=$$\lambda$$$$\nabla$$g(x,y)3. Finding the gradients for f and g and using the above formula, I obtained the following system of equations:
-5/x^2=$$\lambda$$
-1/y^2=$$\lambda$$

Solving for x and y,
x=$$\sqrt{-5/lambda$$ and
y=$$\sqrt{-1/lambda$$

I discarded the negative valued solutions for x and y because of the given constraints that x and y are both greater than 0.

the constraint restated:
x+y=1

substituting x and y into this expression to solve for $$\lambda$$,
I get $$\lambda$$=-2(3+sqrt{5})

solving for the numerical values of x and y using this $$\lambda$$,
I get that
x=sqrt(-5/(2(3+sqrt5))) and
y=sqrt(-1/(2(3+sqrt5)))

Plugging these values into f(x,y)=5/x+1/y I get a value of about 10.47.
I assume this to be a max since the other solutions for x and y (the negative values of what I found for x and y) had to be discarded due to the constraints that x and y > 0. These discarded x and y values would have produced a value less than 10.47, so I conclude that 10.47 is the max. Any input? Corrections? I expect more of the latter, haha.