Laplace transform of ##f(t)=(u(t)-u(t-2\pi))\sin{t}##

[zenterix]

Homework Statement

Find the Laplace transform of $f(t)=(u(t)-u(t-2\pi))\sin{t}$ by use of the $t$-shift rule.

Relevant Equations

$$\mathcal{L}(u(t-a)f(t-a))=e^{-as}\mathcal{L}(f(t))$$

$$\mathcal{L}(u(t-a)f(t))=e^{-as}\mathcal{L}(f(t+a))$$

I tried to solve this as follows

$$f(t)=(u(t)-u(t-2\pi))\sin{t}$$

$$=u(t)\sin{t}-u(t-2\pi)\sin{t}$$

$$\mathcal{L}(f(t))=e^{0\cdot s}\mathcal{sin{t}}-e^{-2pi s}\mathcal{L}(\sin{(t+2\pi)})$$

$$=\frac{1-e^{-2\pi s}}{s^2+1}$$

where I used the fact that $\sin{(t+2\pi)}=\sin{t}$.

Then I looked at the solution and it has the following

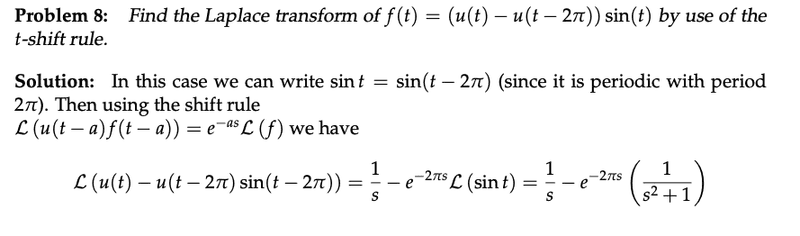
I don't understand this solution.

First of all, in $\mathcal{L}(u(t)-u(t-2\pi)\sin{(t-2\pi)})$ why is there no $\sin{t}$ multiplying the $u(t)$?

 

[Orodruin]

First of all, in $\mathcal{L}(u(t)-u(t-2\pi)\sin{(t-2\pi)})$ why is there no $\sin{t}$ multiplying the $u(t)$?

Because sometimes there are errors in the provided solutions.