Laplace Transformation Help: Simplifying Denominators and Finding Solutions

[stef6987]

1. Homework Statement [/b]

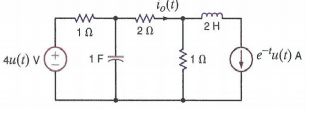
I'm required to find the current i0(t), i wrote KVL equations for each loop, I0 can be expressed interms of i1 and i3, i3 being the current source on the right. i managed to get the solution down to the following :

i0 = (s + 4)/(3*s^2 + 4*s + 1)

I simplified the denominator by completing the square and got:

i0 = (s + 4)/((3*(s+4/6)^2 - 12/36))

Now I'm kind of stuck, i one of solutions is in the form (s+a)/((s+a)^2 + w^2) I'm not sure how i can get my solution to be similar to this, any tips would be awesome :)
thankyou!

Homework Equations

The Attempt at a Solution

 

[gneill]

Can you show your initial loop equations? I'm not seeing the same result that you have for i_o.

(Try using the x² and x₂ icons in the edit panel header to produce exponents and subscripts )

 

[stef6987]

hmm i think i made a few mistakes, i tried it again and this is what i get :

kvl 1:
-4/s + i1 + i1/s - i0/s
=> 4/s = i1 + i1/s - i0/s

kvl 2:
2io + io - 1/(s+1) + i0/s - i1/s = 0

Now i rearranged kvl 2 to find i1 and i got:
i1/s = 3i0 - 1/(s+1) + i0/s
= i0(3 + 1/s) - 1/(s+1)
i1 = s(i0(3+1/s) - 1(s+1)) = i0(3s + 1) - s/(s+1)

so how i got my original answer is a bit of a mystery haha. I tried it again and substituted i1 into kvl 1 and got the answer from wolphram alpha

(s+4)/(3s² + 4s)

Is this what you got?

 

[gneill]

Yup, that's what I found.

 

[stef6987]

Ok, now that i got that right :P i need to convert it back to the time domain, but no solution in my list seems to match. any ideas?

 

[stef6987]

ahh, the answer was so simple, i used the inverse laplace transformation

the equation is in the form:

s+4 = A/s + B/(3s+4)
A = 1
B = -2

1/s = u(t)
B/(3(s+4/3) = -2e^-(4/3)t*(3)

i'm not to sure do i just multiply the 3 to the equation?

 

[gneill]

I suspect that the 3 should divide the equation, not multiply. And the u(t) should be transformed, too.

 

[stef6987]

well A = 1, 1/s = u(t) so what else could i do to that?
my final solution was:

1/u(t) - (2/3)*e^-(4/3)t/(s+(4/3))

 

[gneill]

There should be no s's in the time domain result, only t's and constants. If time is assumed to begin at t=0 for the circuit, the u(t) becomes a constant 1.

 

[stef6987]

Oh ok i think i follow, i realized i had a small mistake (not sure why i had the extra s ahah) it should be:

u(t) - (2/3)*e^-(4/3)t

i need to find I for t>0, so at t>0 u(t) = 1, is that what you're implying?

so my answer should be:

1 - (2/3)*e^-(4/3)t

 

[gneill]

That looks good to me