- #1
MaxR2018
- 5
- 0
New poster has been reminded to use the Homework Help Template in the schoolwork forums
Hi, i need some help here. Can you help me?
Here is the problem.
Exercise statement: The switch have been closed for a long time y is opened at t=0. Using Laplace's transtormation calculate V0(t) for t ≥ 0
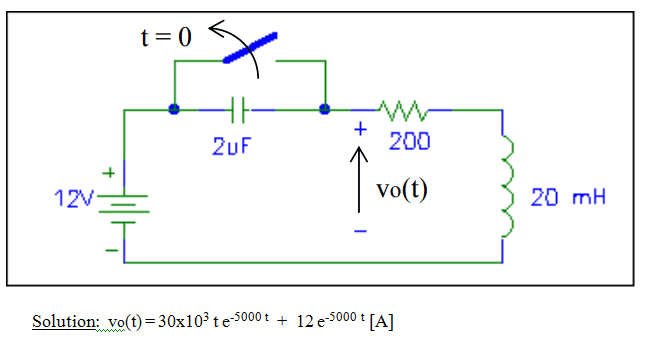 This is what i made to solve it:
This is what i made to solve it:
1) I know while the switch is closed, the current trough the circuit is i=12v/200, so i=60mA.
2) When the switch is opened at t=0, i use the voltages law of kirchoff:
12 = vc + vr + vl
12= (1/c)*(integrate of i dt from 0 to t) + vc(0) + iR + L(di/dt)
i know that vc(0) = 0
so : 12= (1/c)*(integrate of i dt from 0 to t) + iR + L(di/dt)
Then i used the laplace transformation:
12/s = I(s)/Sc + RI(S) + LSI(S) - LI(0)
And i know that LI(0)=60mA
so:
12/s = I(s)/Sc + RI(S) + LSI(S) - 60mA
Finally i calculate I(S) and then i obtain i(t) with the antitransformation of Laplace.
Then, with i(t) i calculate vt knowing that:
VL=L*(di/dt), but i obtain a diferent solution.
I obtain that V0(t) = -300000*e^(-5000t) + 12e^(-5000t)
What I am doing wrong??
I thing I am having a mistake with some signs.
Pd: Sorry for my bad english.
Thanks for reading me!

Here is the problem.
Exercise statement: The switch have been closed for a long time y is opened at t=0. Using Laplace's transtormation calculate V0(t) for t ≥ 0
1) I know while the switch is closed, the current trough the circuit is i=12v/200, so i=60mA.
2) When the switch is opened at t=0, i use the voltages law of kirchoff:
12 = vc + vr + vl
12= (1/c)*(integrate of i dt from 0 to t) + vc(0) + iR + L(di/dt)
i know that vc(0) = 0
so : 12= (1/c)*(integrate of i dt from 0 to t) + iR + L(di/dt)
Then i used the laplace transformation:
12/s = I(s)/Sc + RI(S) + LSI(S) - LI(0)
And i know that LI(0)=60mA
so:
12/s = I(s)/Sc + RI(S) + LSI(S) - 60mA
Finally i calculate I(S) and then i obtain i(t) with the antitransformation of Laplace.
Then, with i(t) i calculate vt knowing that:
VL=L*(di/dt), but i obtain a diferent solution.
I obtain that V0(t) = -300000*e^(-5000t) + 12e^(-5000t)
What I am doing wrong??
I thing I am having a mistake with some signs.
Pd: Sorry for my bad english.
Thanks for reading me!
