Lennard-Jones Potential: Derive an expression for equilibrium constant

[Flucky]

Edit: well this is frustrating, not sure why the itex things aren't working..

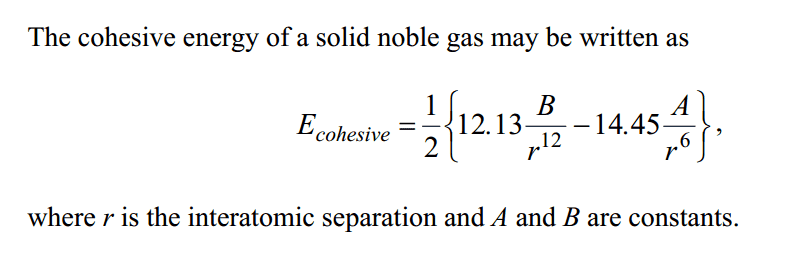
Edit2: I've attached a picture of the question at the bottom as well.

Homework Statement

The cohesive energy of a solid noble gas may be written as

(See picture below)

Derive an expression for the equilibrium separation r₀ of the atoms.

The Attempt at a Solution

At E_cohesive, r=r₀ and dE/dr₀ = 0

So first I rearranged the main equation into something nicer to differentiate:

E = 6.065Br^{-12}_{0} - 7.225Ar^{-6}_{0}

Then differentiated:

dE/dr₀ = -72.78\frac{B}{r^{13}_{0}} + 43.35\frac{A}{r^{7}_{0}} = 0

43.35\frac{A}{r^{7}_{0}} = 72.78\frac{B}{r^{13}_{0}}

r^{6}_{0} = \frac{72.78}{43.35}\frac{B}{A}

So r₀ = (\frac{72.78}{43.35}\frac{B}{A})^\frac{1}{6}

But this looks pretty horrible, is it any good?

Cheers.

-------------------------------------------------------------------------------------------

 

[Flucky]

Finally found a similar question in the depths of the internet and looks like it is right, so all is good here.