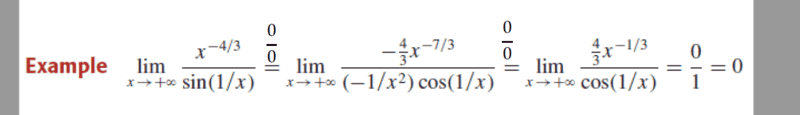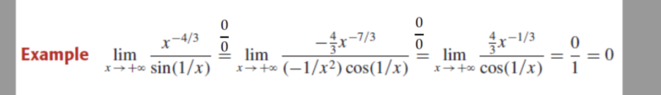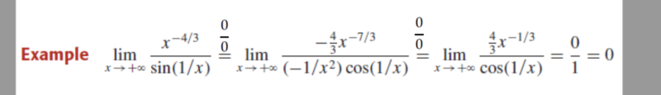SUMMARY
The discussion centers on the application of L'Hopital's Rule to evaluate the limit of the function x^(-4/3) as x approaches infinity. Participants confirm that as x increases indefinitely, the term x^(4/3) approaches positive infinity, leading to its inverse, x^(-4/3), approaching zero. This conclusion is established through the mathematical principles governing limits and the behavior of polynomial functions at infinity.
PREREQUISITES
- Understanding of limits in calculus
- Familiarity with L'Hopital's Rule
- Knowledge of polynomial functions
- Basic algebraic manipulation skills
NEXT STEPS
- Study the detailed application of L'Hopital's Rule in various limit scenarios
- Explore the behavior of polynomial functions at infinity
- Learn about other limit evaluation techniques, such as epsilon-delta proofs
- Investigate the implications of limits in real-world applications
USEFUL FOR
Students of calculus, mathematics educators, and anyone seeking to deepen their understanding of limits and L'Hopital's Rule in mathematical analysis.