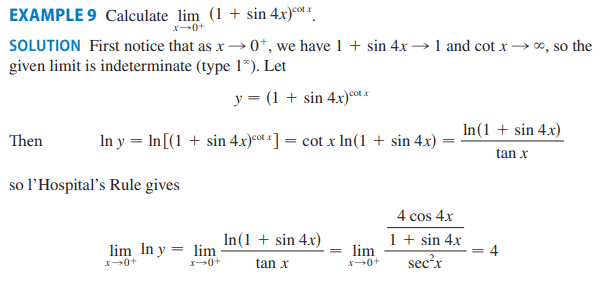SUMMARY
The discussion centers on the application of L'Hôpital's Rule and the continuity of logarithmic and exponential functions in evaluating limits. Participants confirm that if the limit of the logarithm of a function approaches 4, then the limit of the original function is e4. The key point is the ability to swap the limit and logarithm due to the continuity of the natural logarithm and the exponential function, which allows for the transformation of the limit expression. This swapping is crucial for simplifying the evaluation of indeterminate forms.
PREREQUISITES
- Understanding of L'Hôpital's Rule
- Knowledge of limits and continuity in calculus
- Familiarity with logarithmic and exponential functions
- Basic skills in manipulating indeterminate forms
NEXT STEPS
- Study the application of L'Hôpital's Rule in various indeterminate forms
- Learn about the continuity properties of logarithmic and exponential functions
- Explore advanced limit techniques, including epsilon-delta definitions
- Review examples of limits involving exponential expressions and logarithms
USEFUL FOR
Students and educators in calculus, mathematicians dealing with limits, and anyone seeking to understand the application of L'Hôpital's Rule in evaluating indeterminate forms.