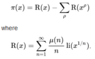- #1
nomadreid
Gold Member
- 1,668
- 203
Extremely quick question:
According to http://mathworld.wolfram.com/PrimeNumberTheorem.html, the Riemann Hypothesis is equivalent to
|Li(x)-π(x)|≤ c(√x)*ln(x) for some constant c.
Am I correct that then c goes to 0 as x goes to infinity?
Does any expression exist (yet) for c?
Thanks.
According to http://mathworld.wolfram.com/PrimeNumberTheorem.html, the Riemann Hypothesis is equivalent to
|Li(x)-π(x)|≤ c(√x)*ln(x) for some constant c.
Am I correct that then c goes to 0 as x goes to infinity?
Does any expression exist (yet) for c?
Thanks.